8 câu hỏi trắc nghiệm thuộc Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 4)

Câu 1:

Cho các biểu thức:

$A = 3 \sqrt{3} - \sqrt{50} - \sqrt{{(\sqrt{2} - 1)}^{2}}$ ;

$B = (\frac{3 \sqrt{x} + 6}{x - 4} + \frac{\sqrt{x}}{\sqrt{x} - 2}) : \frac{x - 9}{\sqrt{x} - 3}$ với $x \geq 0; x \neq 4; x \neq 9.$

1) Rút gọn biểu thức A và B

2) Tìm x sao cho A - 2B = 3

Xem đáp án

a) $A = 3 \sqrt{3} - \sqrt{50} - \sqrt{{(\sqrt{2} - 1)}^{2}} = 6 \sqrt{2} - 5 \sqrt{2} - |\sqrt{2} - 1|$ $= \sqrt{2} - \sqrt{2} + 1 = 1$ (vì $\sqrt{2} - 1 > 0) .$

Với $x \geq 0; x \neq 4; x \neq 9,$ ta có:

$B = (\frac{3 \sqrt{x} + 6}{x - 4} + \frac{\sqrt{x}}{\sqrt{x} - 2}) : \frac{x - 9}{\sqrt{x} - 3} = [\frac{3 (\sqrt{x} + 2)}{(\sqrt{x} + 2) (\sqrt{x} - 2)} + \frac{\sqrt{x}}{\sqrt{x} - 2}] : \frac{(\sqrt{x} + 3) (\sqrt{x} - 3)}{\sqrt{x} - 3} = (\frac{3}{\sqrt{x} - 2} + \frac{\sqrt{x}}{\sqrt{x} - 2}) : (\sqrt{x} + 3) = \frac{\sqrt{x} + 3}{\sqrt{x} - 2} \cdot \frac{1}{\sqrt{x} + 3} = \frac{1}{\sqrt{x} - 2}$

b) Để $A - 2 B = 3$ thì $1 - \frac{2}{\sqrt{x} - 2} = 3 \Rightarrow \sqrt{x} - 2 - 2 = 3 \sqrt{x} - 6$

$\Leftrightarrow 2 \sqrt{x} = 2 \Leftrightarrow \sqrt{x} = 1 \Leftrightarrow x = 1$ (thỏa mãn)

Vậy x = 1 thì A - 2B = 3

Câu 2:

Giải hệ phương trình

\{\begin{cases} 2 (x - 3) + 3 (3 x + y) = - 11 \\ (x - 3) - 2 (3 x + y) = 5 \end{cases} .

Xem đáp án

$\{\begin{cases} 2 (x - 3) + 3 (3 x + y) = - 11 \\ (x - 3) - 2 (3 x + y) = 5 \end{cases} \Leftrightarrow \{\begin{cases} 4 (x - 3) + 6 (3 x + y) = - 22 \\ 3 (x - 3) - 6 (3 x + y) = 15 \end{cases} \Leftrightarrow \{\begin{cases} 7 (x - 3) = - 7 \\ (x - 3) - 2 (3 x + y) = 5 \end{cases} \Leftrightarrow \{\begin{cases} x - 3 = - 1 \\ (x - 3) - 2 (3 x + y) = 5 \end{cases} \Leftrightarrow \{\begin{cases} x - 3 = - 1 \\ (x - 3) - 2 (3 x + y) = 5 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ (2 - 3) - 2 (3 \cdot 2 + y) = 5 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ 6 + y = - 3 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = - 9 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất là

(x; y) = (2; - 9)

Câu 3:

Một quyển vở giá 14 000 đồng, một hộp bút giá 30 000 đồng. Minh muốn mua một hộp bút và một số quyển vở.

a) Gọi $x (x \in ℕ *)$ là số quyển vở Minh mua, y là số tiền cần trả khi mua x quyển vở và một hộp bút. Hãy biểu diễn y theo x

b) Nếu Minh có 300 000 đồng để mua vở và một hộp bút thì Minh mua được tối đa bao nhiêu quyển vở?

Xem đáp án

a) Số tiền cần phải trả khi mua x quyển vở là: $14 000 x$ (đồng).

Số tiền y cần trả khi mua x quyển vở và một hộp bút là $y = 14 000 x + 30 000$ (đồng).

b) Theo đề bài, ta có: $14 000 x + 30 000 \leq 300 000$

$\Leftrightarrow 14 000 x \leq 270 000 \Leftrightarrow x \leq \frac{135}{7} \approx 19, 29$

Vậy bạn Minh mua tối đa được 19 quyển vở.

Câu 4:

Cho phương trình $x^{2} - 2 (m - 1) x + m^{2} - 9 = 0$ (1) x là ẩn, m là tham số).

a) Giải phương trình (1) khi m = -3

b) Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn điều kiện $x_{1} - x_{2} = 2 m - 10.$

Xem đáp án

a) Với $m = - 3$ phương trình (1) có dạng:

$x^{2} + 8 x = 0 \Leftrightarrow x (x + 8) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x + 8 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = - 8 \end{array}$

Vậy khi $m = - 3,$ phương trình có nghiệm là $x = 0; x = - 8.$

b) Ta có $Δ^{'} = {[- (m - 1)]}^{2} - m^{2} + 9 = m^{2} - 2 m + 1 - m^{2} + 9 = - 2 m + 10$ .

Phương trình (1) có hai nghiệm phân biệt $x_{1}, x_{2}$ khi và chỉ khi $Δ^{'} > 0 \Leftrightarrow - 2 m + 10 > 0 \Leftrightarrow m < 5.$

Theo định lí Vi-et, ta có: $\{\begin{cases} x_{1} + x_{2} = 2 (m - 1) (2) \\ x_{1} x_{2} = m^{2} - 9 (3) \end{cases}$

Theo đề bài, ta có: $x_{1} - x_{2} = 2 m - 10$ , kết hợp với (2) ta được: $x_{1} = 2 m - 6; x_{2} = 4$ .

Thay $x_{1} = 2 m - 6; x_{2} = 4$ vào (3) ta được:

$(2 m - 6) 4 = m^{2} - 9 \Leftrightarrow m^{2} - 8 m + 15 = 0 \Leftrightarrow m = 3$ (thỏa mãn) hoặc m = 5 (loại).

Vậy với m = 3 thì phương trình (1) có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn $x_{1} - x_{2} = 2 m - 10.$

Câu 5:

Một trường học có mảnh vườn hình chữ nhật chu vi 100 m Nhà trường tiến hành mở rộng mảnh vườn đó bằng cách tăng chiều dài thêm 5 m và chiều rộng thêm 4 m khi đó diện tích tăng thêm 240 m² . Tính chiều dài và chiều rộng của mảnh vườn trước khi mở rộng.

Xem đáp án

Gọi chiều dài, chiều rộng của mảnh vườn ban đầu lần lượt là $x (m), y (m) (0 < y < x < 50) .$

Diện tích mảnh vườn ban đầu là xy (m2).

Vì chu vi của mảnh vườn ban đầu là 100 m nên ta có phương trình:

$2 (x + y) = 100 \Leftrightarrow x + y = 50 (1)$

Chiều dài của mảnh vườn sau khi mở rộng là: $(x + 5) (m)$

Chiều rộng của mảnh vườn sau khi mở rộng là: $(y + 4) (m)$

Diện tích mảnh vườn sau khi mở rộng là: $(x + 5) (y + 4)$ (m2).

Do diện tích mảnh vườn đã tăng thêm $240 m^{2}$ nên ta có phương trình

$(x + 5) (y + 4) - x y = 240 (2)$

Từ (1) và (2) ta có hệ phương trình $\{\begin{cases} x + y = 50 \\ (x + 5) (y + 4) - x y = 240 \end{cases}$

$\Leftrightarrow \{\begin{cases} x + y = 50 \\ x y + 4 x + 5 y + 20 - x y = 240 \end{cases} \Leftrightarrow \{\begin{cases} x + y = 50 \\ 4 x + 5 y = 220 \end{cases}$

$\Leftrightarrow \{\begin{cases} 4 x + 4 y = 200 \\ 4 x + 5 y = 220 \end{cases} \Leftrightarrow \{\begin{cases} x + y = 50 \\ y = 20 \end{cases} \Leftrightarrow \{\begin{cases} x = 30 \\ y = 20 \end{cases}$ (thỏa mãn)

Vậy chiều dài, chiều rộng của mảnh vườn ban đầu lần lượt là 30 m và 20 m

Câu 6:

Một chi tiết máy gồm một phân có dạng hình trụ, phần còn lại có dạng hình nón với các kích thước như vẽ. Biết rằng phần hình trụ có chu vi đáy là 37,68 m. Tính thể tích của chi tiết máy đó (lấy $π \approx 3, 14;$ kết quả làm tròn đến chữ số thập phân thứ hai).

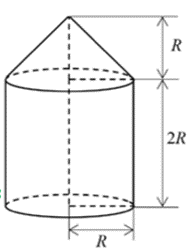
Một chi tiết máy gồm một phân có dạng hình trụ, phần còn lại có dạng hình nón với các kích thước như vẽ. Biết rằng phần hình trụ có chu vi đáy là 37,68 m. (ảnh 1)

Xem đáp án

Độ dài bán kính của hình trụ là: $R \approx \frac{27, 68}{2 \cdot 3, 14} \approx 6 (cm).$

Thể tích của phần có dạng hình trụ là:

$V_{1} = π R^{2} \cdot 2 R \approx 3, 14 \cdot 6^{2} \cdot (2 \cdot 6) \approx 1356, 48 ({cm}^{3}) .$

Thể tích của phần có dạng hình nón là: $V_{2} = \frac{1}{3} π R^{2} \cdot R \approx 3, 14 \cdot 6^{2} \cdot 6 \approx 226, 08 ({cm}^{3}) .$

Thể tích của chi tiết máy đó là: $V = V_{1} + V_{2} \approx 1582, 56 ({cm}^{3}) .$

Câu 7:

Cho đường tròn (O;R) và điểm A sao cho OA > 2R vẽ hai tiếp tuyến AB, AC của đường tròn (B, C là các tiếp điểm), kẻ dây cung BD song song với AC. Đường thẳng AD cắt (O;R) tại điểm $E (E \neq D) .$ Gọi I là trung điểm của DE

1) Chứng minh năm điểm A, B, I, O, C cùng thuộc một đường tròn.

2) Đường thẳng BC cắt OA, AD lần lượt tại H và K. Gọi F là giao điểm của BE và AC Chứng minh AK.AI = AH.AO và tam giác AFE đồng dạng với tam giác BFA

3) Chứng minh ba đường thẳng AB, CD, FK đồng quy.

Xem đáp án

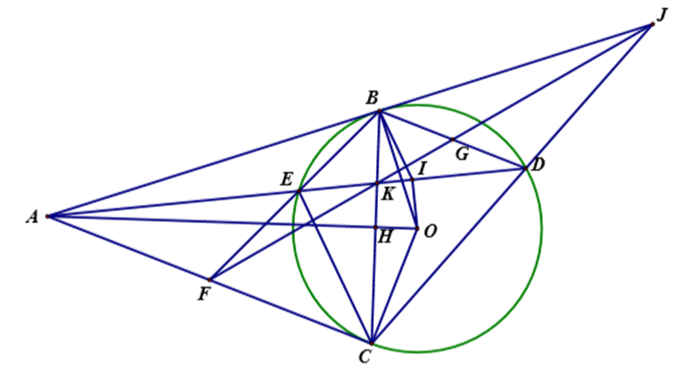
Cho đường tròn (O;R) và điểm A sao cho OA > 2R vẽ hai tiếp tuyến AB, AC của đường tròn (B, C là các tiếp điểm), kẻ dây cung BD song song với AC. Đường thẳng AD cắt (O;R (ảnh 1)

a) Xét đường tròn (O) có:

• DE là dây không đi qua tâm O và I là trung điểm của DE

Suy ra $O I ⊥ D E$ tại I (quan hệ vuông góc giữa đường kính và dây) nên $\hat{A I O} = 90 ° .$

• AB, AC là tiếp tuyến của đường tròn (O) nên $A B ⊥ O B, A C ⊥ O C$ (tính chất tiếp tuyến)

Suy ra $\hat{A B O} = \hat{A C O} = 90 ° .$ Do đó $\hat{A B O} = \hat{A C O} = \hat{A I O} = 90 ° .$

Vậy năm điểm A, B, I, O, C cùng thuộc một đường tròn đường kính AO

b) Xét đường tròn (O;R) có AB = AC (tính chất hai tiếp tuyến cắt nhau)

Mà $O B = O C = R$ nên OA là đường trung trực của BC

Do đó $O A ⊥ B C$ tại H hay $\hat{A H K} = 90 ° .$

Xét $Δ A H K$ và $Δ A I O$ có: $\hat{A H K} = \hat{A I O} = 90 °$ và $\hat{H A K}$ là góc chung

Do đó $Δ A H K ∽ Δ A I O (g.g).$ Suy ra $\frac{A H}{A I} = \frac{A K}{A O}$ hay $A K \cdot A I = A H \cdot A O .$

Ta có BD // AC nên $\hat{B D E} = \hat{F A E}$ (hai góc so le trong)

Mà $\hat{B D E} = \hat{F B A}$ (cùng chắn $\overset{⏜}{E B}$ của $(O; R))$ nên $\hat{F A E} = \hat{F B A} .$

Xét $Δ A F E$ và $Δ B F A$ có: $\hat{A F E}$ là góc chung và $\hat{F A E} = \hat{F B A} .$

Do đó $Δ A F E ∽ Δ B F A (g.g).$

c) Ta có $Δ A F E ∽ Δ B F A$ (câu b) suy ra $\frac{F E}{F A} = \frac{F A}{F B}$ hay $F A^{2} = F B \cdot F E . (1)$

Xét $Δ F E C$ và $Δ F C B$ có: $\hat{E F C}$ là góc chung và $\hat{F C E} = \hat{F B C}$ (cùng chắn $\overset{⏜}{E C}$ của $(O; R))$

Do đó $Δ F E C ∽ Δ F C B (g.g).$ Suy ra $\frac{F E}{F C} = \frac{F C}{F B}$ hay $F C^{2} = F B \cdot F E . (2)$

Từ (1) và (2) suy ra $F A^{2} = F C^{2}$ nên FA = FC. Do đó F là trung điểm của đoạn thẳng AC

Gọi G là giao điểm của FK và BD

Ta có BG // FC suy ra $\frac{B G}{F C} = \frac{K G}{K F}$ (hệ quả định lí Thalès);

DG // AF suy ra $\frac{D G}{A F} = \frac{K G}{K F}$ (hệ quả định lí Thalès).

Suy ra $\frac{B G}{F C} = \frac{D G}{A F}$ mà AF = CF nên BG = DG. Do đó G là trung điểm của BD

Kéo dài AB cắt D tại J. Gọi G' là giao điểm của JF và BD.

• Xét $Δ J A F$ có BG' // AF nên ta có: $\frac{B G^{'}}{A F} = \frac{J G^{'}}{J F}$ (hệ quả định lí Thalès);

• Xét $Δ J F C$ có DG' // CF nên ta có: $\frac{D G^{'}}{C F} = \frac{J G^{'}}{J F}$ (hệ quả định lí Thalès).

Do đó $\frac{B G^{'}}{A F} = \frac{D G^{'}}{C F}$ mà AF = CF nên BG' = DG'

Khi đó G' là trung điểm của BD nên $G^{'} \equiv G .$

Do đó ba điểm F, K, J thẳng hàng.

Vậy ba đường thẳng AB, CD, FK đồng quy.

Câu 8:

Cho các số thực a, b thoả mãn: a > 0, b > 0 và ${(a + b)}^{3} = 2 (1 - a^{2} - b^{2}) .$ Tìm giá trị nhỏ nhất của biểu thức $M = \frac{1}{a b} + \frac{1}{a^{2} + b^{2}}$ .

Xem đáp án

Ta có ${(a + b)}^{3} = 2 (1 - a^{2} - b^{2}) \Leftrightarrow {(a + b)}^{3} + 2 (a^{2} + b^{2}) = 2.$

Vì a > 0, b > 0 ta có $2 (a^{2} + b^{2}) \geq {(a + b)}^{2}$ (theo AM – GM)

$\Rightarrow {(a + b)}^{3} + {(a + b)}^{2} \leq 2 \Leftrightarrow {(a + b)}^{3} + {(a + b)}^{2} - 2 \leq 0 \Leftrightarrow (a + b - 1) [{(a + b)}^{2} + 2 (a + b) + 2] \leq 0$

$\Leftrightarrow a + b - 1 \leq 0$ (vì ${(a + b)}^{2} + 2 (a + b) + 2 > 0$ với a > 0, b > 0)

Chứng minh bất đẳng thức phụ sau: $\frac{1}{x} + \frac{1}{y} \geq \frac{4}{x + y} (x > 0, y > 0) (*)$

Ta có $\frac{1}{x} + \frac{1}{y} \geq \frac{4}{x + y} \Leftrightarrow {(x + y)}^{2} \geq 4 x y \Leftrightarrow {(x - y)}^{2} \geq 0$ (luôn đúng)

Áp dụng bất đẳng thức (*), ta được:

$\frac{1}{a b} + \frac{1}{a^{2} + b^{2}} \geq \frac{4}{a^{2} + b^{2} + 2 a b} \Leftrightarrow \frac{1}{2 a b} + \frac{1}{a^{2} + b^{2}} \geq \frac{4}{{(a + b)}^{2}} \geq 4$ (vì $a + b \leq 1$ )

Với $a > 0, b > 0$ , ta có $1 \geq a + b \geq 2 \sqrt{a b} \Rightarrow 1 \geq 4 a b \Rightarrow \frac{1}{2 a b} \geq 2.$

Khi đó $M = \frac{1}{a b} + \frac{1}{a^{2} + b^{2}} = (\frac{1}{2 a b} + \frac{1}{a^{2} + b^{2}}) + \frac{1}{2 a b} \geq 4 + 2 \Leftrightarrow M \geq 6.$

Dấu "=" xảy ra khi và chỉ khi $a = b = \frac{1}{2} .$

Vậy giá trị nhỏ nhất của M là 6 khi và chỉ khi $a = b = \frac{1}{2} .$