Trắc nghiệm Toán 9 Cánh diều tạo Bài 2. Một số phép tính về căn bậc hai của số thực có đáp án
Trắc nghiệm Toán 9 Cánh diều tạo Bài 2. Một số phép tính về căn bậc hai của số thực có đáp án
-
61 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Với hai số thực \(a,\,\,b\) không âm thì \[\sqrt {a \cdot b} \] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Với hai số thực \(a,\,\,b\) không âm thì \[\sqrt {a \cdot b} = \sqrt a \cdot \sqrt b \].
Câu 2:
Biểu thức \(\sqrt 3 \cdot \sqrt {16} \cdot \sqrt {14} \) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có \(\sqrt 3 \cdot \sqrt {16} \cdot \sqrt {14} = \sqrt {3 \cdot 16 \cdot 14} \).
Câu 3:
Với số thực \(a\) không âm và số thực \(b\) dương thì \[\sqrt {\frac{a}{b}} \] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Với số thực \(a\) không âm và số thực \(b\) dương, ta có \[\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\].
Câu 4:
Cho ba số \(a \ge 0\) và \(b > 0,\,\,c > 0\). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Với ba số \(a \ge 0\) và \(b > 0,\,\,c > 0\), ta có:
⦁ \(\sqrt {ab} = \sqrt a \cdot \sqrt b ;\)
⦁ \(\frac{{\sqrt {ab} }}{{\sqrt c }} = \sqrt {\frac{{ab}}{c}} ;\)
⦁ \(\frac{{\sqrt a }}{{\sqrt {bc} }} = \sqrt {\frac{a}{{bc}}} \).
Vậy cả A, B, C đều đúng. Ta chọn phương án D.
Câu 5:
Cho số \(a \ge 0.\) Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Với \(a \ge 0,\) ta có: \(\sqrt {{a^2}} = \left| a \right| = a.\)
Câu 6:
II. Thông hiểu
Rút gọn biểu thức \(A = \sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} - \sqrt 2 \) ta được
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \(A = \sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} - \sqrt 2 = \left| {1 - \sqrt 2 } \right| - \sqrt 2 = \sqrt 2 - 1 - \sqrt 2 = - 1.\)
Câu 7:
Biết \(\sqrt {ab} = \sqrt { - a} \cdot \sqrt { - b} \) với hai số \(a \ne 0,\,\,b \ne 0\) và cho các khẳng định sau:
(i) Số \(a\) là số âm.
(ii) Số \(a\) và \(b\) có cùng dấu.
(iii) Số \(a\) và \(b\) là hai số được biểu diễn trên trục số bởi các điểm nằm bên trái số 0.
Có bao nhiêu khẳng định sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Từ \(\sqrt {ab} = \sqrt { - a} \cdot \sqrt { - b} \) ta có \(a\) và \(b\) cùng là số âm. Do đó (i) và (ii) là đúng.
Do \(a\) và \(b\) cùng là số âm nên hai số này được biểu diễn trên trục số bởi các điểm nằm bên trái số 0. Do đó (iii) là đúng. Như vậy, không có khẳng định nào sai.
Vậy ta chọn phương án A.
Câu 8:
Cho hai số \(a < 0\) và \(b \ge 0.\) Khẳng định nào sau đây là đúng?
</>
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Với \(a < 0\) và \(b \ge 0,\) ta có: \(\sqrt {{a^2}b} = \sqrt {{a^2}} \cdot \sqrt b = \left| a \right|\sqrt b = - a\sqrt b .\)
Câu 9:
Giá trị của biểu thức \(\left( {\sqrt {\frac{2}{3}} + \sqrt {\frac{{50}}{3}} - \sqrt {24} } \right) \cdot \sqrt 6 \) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Cách 1. Ta có:
\(\left( {\sqrt {\frac{2}{3}} + \sqrt {\frac{{50}}{3}} - \sqrt {24} } \right) \cdot \sqrt 6 \)
\[ = \sqrt {\frac{2}{3}} \cdot \sqrt 6 + \sqrt {\frac{{50}}{3}} \cdot \sqrt 6 - \sqrt {24} \cdot \sqrt 6 \]
\( = \sqrt {\frac{2}{3} \cdot 6} + \sqrt {\frac{{50}}{3} \cdot 6} - \sqrt {24 \cdot 6} \)
\( = \sqrt 4 + \sqrt {100} - \sqrt {144} \)
\[ = 2 + 10--12 = 0.\]
Cách 2. Sử dụng máy tính cầm tay.
Ta lần lượt bấm các phím:

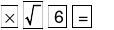
Trên màn hình ta nhận được kết quả là 0.
Vậy ta chọn phương án B.
Câu 10:
Với số \(a > 0\) thì giá trị của biểu thức \(\sqrt {6a} \cdot \sqrt {\frac{1}{{6{a^3}}}} \) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Với số \(a > 0\), ta có: \(\sqrt {6a} \cdot \sqrt {\frac{1}{{6{a^3}}}} \)\( = \sqrt {6a \cdot \frac{1}{{6{a^3}}}} = \sqrt {\frac{1}{{{a^2}}}} = \frac{{\sqrt 1 }}{{\sqrt {{a^2}} }} = \frac{1}{{\left| a \right|}} = \frac{1}{a}.\)
Câu 11:
Với số \(a\) dương thì biểu thức \[\frac{{\sqrt {{a^6}} }}{{\sqrt {{a^4}} }} - \frac{{\sqrt {{a^3}} }}{{\sqrt a }}\] có giá trị là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Với số \(a\) dương, ta có: \[\frac{{\sqrt {{a^6}} }}{{\sqrt {{a^4}} }} - \frac{{\sqrt {{a^3}} }}{{\sqrt a }}\]\( = \sqrt {\frac{{{a^6}}}{{{a^4}}}} - \sqrt {\frac{{{a^3}}}{a}} \)\[ = \sqrt {{a^2}} - \sqrt {{a^2}} = 0.\]
Câu 12:
Với hai số \(a < 0,\,\,b > 0\), biểu thức \[ - \frac{1}{3}a{b^3} \cdot \sqrt {\frac{{9{a^2}}}{{{b^6}}}} \] có giá trị là</>
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Với hai số \(a < 0,\,\,b > 0\), ta có:</>
\[ - \frac{1}{3}a{b^3} \cdot \sqrt {\frac{{9{a^2}}}{{{b^6}}}} \]\[ = - \frac{1}{3}a{b^3} \cdot \frac{{\sqrt {9{a^2}} }}{{\sqrt {{b^6}} }}\]\[ = - \frac{1}{3}a{b^3} \cdot \frac{{\sqrt {{{\left( {3a} \right)}^2}} }}{{\sqrt {{{\left( {{b^3}} \right)}^2}} }}\]\[ = - \frac{1}{3}a{b^3} \cdot \frac{{\left| {3a} \right|}}{{\left| {{b^3}} \right|}}\]\[ = - \frac{1}{3}a{b^3} \cdot \frac{{ - 3a}}{{{b^3}}}\]\( = {a^2}\).
Câu 13:
III. Vận dụng
Cho biểu thức \(A = \sqrt {20 + \sqrt {20 + \sqrt {20 + ...} } } \)(có vô hạn số \(\sqrt {20} ).\) Giá trị của biểu thức \(A\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có \(A = \sqrt {20 + \sqrt {20 + \sqrt {20 + ...} } } > 0\) nên:
\({A^2} = {\left( {\sqrt {20 + \sqrt {20 + \sqrt {20 + ...} } } } \right)^2} = 20 + \sqrt {20 + \sqrt {20 + ...} } = 20 + A\)
Suy ra \({A^2} - A - 20 = 0\)
\({A^2} - 5A + 4A - 20 = 0\)
\(A\left( {A - 5} \right) + 4\left( {A - 5} \right) = 0\)
\(\left( {A - 5} \right)\left( {A + 4} \right) = 0\)
\(A - 5 = 0\) (vì \(A > 0\) nên \(A + 4 > 0)\)
\(A = 5.\)
Vậy ta chọn phương án D.
Câu 14:
Khi một quả bóng rổ được thả xuống, nó sẽ nảy trở lại, nhưng do tiêu hao năng lượng nên nó không đạt được chiều cao như lúc bắt đầu. Hệ số phục hồi của quả bóng rổ được tính theo công thức \[{C_R} = \sqrt {\frac{h}{H}} ,\] trong đó \(H\) là độ cao mà quả bóng được thả rơi; \(h\) là độ cao mà quả bóng bật lại. Một quả bóng rổ rơi từ độ cao \[3,24{\rm{ m}}\] và bật lại độ cao \[2,25{\rm{ m}}.\] Hệ số phục hồi của quả bóng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Thay \[H = 3,24\,\,{\rm{m}}\] và \[h = 2,25\,\,{\rm{m,}}\] ta được:
\[{C_R} = \sqrt {\frac{h}{H}} = \sqrt {\frac{{2,25}}{{3,24}}} = \sqrt {\frac{{225}}{{324}}} = \frac{{\sqrt {225} }}{{\sqrt {324} }} = \frac{{15}}{{18}} = \frac{5}{6}\].
Vậy hệ số phục hồi của quả bóng là \({C_R} = \frac{5}{6}\).
Câu 15:
Trong Vật lí, ta có định luật Joule – Lenz để tính nhiệt lượng toả ra ở dây dẫn khi có dòng điện chạy qua:
\[Q = {I^2}Rt\].
Trong đó: \[Q\] là nhiệt lượng toả ra trên dây dẫn tính theo Jun (J);
\[I\] là cường độ dòng điện chạy trong dây dẫn tính theo Ampe (A);
\[R\] là điện trở dây dẫn tính theo Ohm (Ω);
\[t\] là thời gian dòng điện chạy qua dây dẫn tính theo giây.
Một bếp điện khi hoạt động bình thường có điện trở \[R = 80\,\,\Omega .\] Biết nhiệt lượng mà dây dẫn toả ra trong 1 giây là 500 J. Cường độ dòng điện chạy trong dây dẫn là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo bài, ta có \[R = 80\,\,\Omega ,\] \[t = 1\] (s), \[Q = 500\] (J).
Thay vào công thức \[Q = {I^2}Rt\], ta có: \[500 = {I^2} \cdot 80 \cdot 1\]
Suy ra \(80{I^2} = 500\), nên \[{I^2} = \frac{{500}}{{80}} = \frac{{25}}{4}\].
Do đó \[I = \sqrt {\frac{{25}}{4}} = \frac{{\sqrt {25} }}{{\sqrt 4 }} = \frac{5}{2} = 2,5\] (A).
Vậy cường độ dòng điện chạy trong dây dẫn là \[2,5\] Ampe.
