23 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 20

Câu 1:

Giải hệ phương trình bằng phương pháp thế :

$\{\begin{cases} 4 x + 5 y = 3 \\ x - 3 y = 5 \end{cases}$

$\{\begin{cases} 4 x + 5 y = 3 \\ x - 3 y = 5 \end{cases} \Leftrightarrow \{\begin{cases} 4 (3 y + 5) + 5 y = 3 \\ x = 3 y + 5 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = - 1 \end{cases}$

Câu 2:

Giải hệ phương trình bằng phương pháp thế :

\{\begin{cases} 7 x - 2 y = 1 \\ 3 x + y = 6 \end{cases}

Xem đáp án

$\{\begin{cases} 7 x - 2 y = 1 \\ 3 x + y = 6 \end{cases} \Leftrightarrow \{\begin{cases} 7 x - 2 (6 - 3 x) = 1 \\ y = 6 - 3 x \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 3 \end{cases}$

Câu 3:

Giải hệ phương trình bằng phương pháp thế :

\{\begin{cases} \sqrt{5} x - y = \sqrt{5} (\sqrt{3} - 1) \\ 2 \sqrt{3} x + 3 \sqrt{5} y = 21 \end{cases}

Xem đáp án

$\{\begin{cases} \sqrt{5} - y = \sqrt{5} (\sqrt{3} - 1) \\ 2 \sqrt{3} x + 3 \sqrt{5} y = 21 \end{cases} \Leftrightarrow \{\begin{cases} y = \sqrt{5} x - \sqrt{15} - \sqrt{5} \\ 2 \sqrt{3} x + 3 \sqrt{5} (\sqrt{5} x - \sqrt{15} - \sqrt{5}) = 21 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{450 - 153 \sqrt{3}}{213} \\ x = \frac{23 \sqrt{5} - 366 \sqrt{15}}{213} \end{cases}$

Câu 4:

Giải hệ phương trình bằng phương pháp thế :

$\{\begin{cases} (\sqrt{5} + 2) x + y = 3 - \sqrt{5} \\ - x + 2 y = 6 - 2 \sqrt{5} \end{cases}$

Xem đáp án

$\begin{array}{l} \{\begin{cases} (\sqrt{5} + 2) x + y = 3 - \sqrt{5} \\ - x + 2 y = 6 - 2 \sqrt{5} \end{cases} \Leftrightarrow \{\begin{cases} y = (\sqrt{5} + 2) x - 3 + \sqrt{5} \\ - x + (2 \sqrt{5} + 4) x - 6 + 2 \sqrt{5} = 6 - 2 \sqrt{5} \end{cases} \\ \Leftrightarrow \{\begin{cases} (2 \sqrt{5} + 3) x = 12 - 4 \sqrt{5} \\ y = (\sqrt{5} + 2) x - 3 + \sqrt{5} \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{- 76 + 36 \sqrt{5}}{11} \\ y = \frac{- 5 + 7 \sqrt{5}}{11} \end{cases} \end{array}$

Câu 5:

Giải hệ phương trình bằng phương pháp thế :

$\{\begin{cases} 3 (y - 5) + 2 (x - 3) = 0 \\ 7 (x - 4) + 3 (x + y - 1) - 14 = 0 \end{cases}$

Xem đáp án

$\{\begin{cases} 3 (y - 5) + 2 (x - 3) = 0 \\ 7 (x - 4) + 3 (x + y - 1) - 14 = 0 \end{cases} \Leftrightarrow \{\begin{cases} 2 x + 3 y = 21 \\ 10 x + 3 y = 45 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 \\ y = 5 \end{cases}$

Câu 6:

Giải hệ phương trình bằng phương pháp thế :

\{\begin{cases} 5 (x + 2 y) - 3 (x - y) = 99 \\ x - 3 y = 7 x - 4 y - 17 \end{cases}

Xem đáp án

$\{\begin{cases} 5 (x + 2 y) - 3 (x - y) = 99 \\ x - 3 y = 7 x - 4 y - 17 \end{cases} \Leftrightarrow \{\begin{cases} 2 x + 13 y = 99 \\ 6 x - y = 17 \end{cases} \Leftrightarrow \{\begin{cases} x = 4 \\ y = 7 \end{cases}$

Câu 7:

Giải hệ phương trình bằng phương pháp thế :

\{\begin{cases} (x + 1) (y - 1) = x y - 1 \\ (x - 3) (y - 3) = x y - 3 \end{cases}

Xem đáp án

$\{\begin{cases} (x + 1) (y - 1) = x y - 1 \\ (x - 3) (y - 3) = x y - 3 \end{cases} \Leftrightarrow \{\begin{cases} x y - x + y - 1 = x y - 1 \\ x y - 3 x - 3 y + 9 = x y - 3 \end{cases} \Leftrightarrow x = y = 2$

Câu 8:

Cho hệ phương trình $\{\begin{cases} (3 a + b) x + (4 a - b + 1) y = 35 \\ b x + 4 a y = 29 \end{cases}$
Tìm các giá trị của a, b để hệ phương trình có nghiệm là (1; -3)

Xem đáp án

Vì hệ có nghiệm $(1; - 3) \Rightarrow \{\begin{cases} x = 1 \\ y = - 3 \end{cases}$ , thay vào:

$\Rightarrow \{\begin{cases} 3 a + b + 3 b - 12 a - 3 = 35 \\ b - 12 a = 29 \end{cases} \Leftrightarrow \{\begin{cases} 9 a - 3 b = - 38 \\ 12 a - b = - 29 \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{- 49}{27} \\ b = \frac{65}{9} \end{cases}$

Câu 9:

Tìm dư của phép chia đa thức $x^{20} + x^{11} + 1996 x$ cho đa thức $x^{2} - 1$

Xem đáp án

Vì đa thức thương là bậc hai đối với x nên gọi đa thức dư khi chia đa thức $x^{20} + x^{11} + 1996 x$ cho đa thức $x^{2} - 1$ là ax + b. Ta có:

$f (x) = (x^{20} + x^{11} + 1996 x) - (a x + b) ⋮ (x^{2} - 1), x^{2} - 1 = (x - 1) (x + 1)$

Do đó $\{\begin{cases} f (1) = 0 \\ f (- 1) = 0 \end{cases} \Leftrightarrow \{\begin{cases} 1998 - (a + b) = 0 \\ - 1996 - (- a + b) = 0 \end{cases} \Leftrightarrow \{\begin{cases} a = 1997 \\ b = 1 \end{cases}$

Đa thức dư là 1997x + 1

Câu 10:

Giải hệ phương trình sau:

$\{\begin{cases} \frac{1}{x - 2} + \frac{1}{2 y - 1} = 2 \\ \frac{2}{x - 2} - \frac{3}{2 y - 1} = 1 \end{cases}$

Xem đáp án

$\{\begin{cases} \frac{1}{x - 2} + \frac{1}{2 y - 1} = 2 \\ \frac{2}{x - 2} - \frac{3}{2 y - 1} = 1 \end{cases} (x \neq 2; y \neq \frac{1}{2})$

Đặt $a = \frac{1}{x - 2}; b = \frac{1}{2 y - 1}$ , hệ phương trình thành:

$\{\begin{cases} a + b = 2 \\ 2 a - 3 b = 1 \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{7}{5} \\ b = \frac{3}{5} \end{cases} \Rightarrow \{\begin{cases} \frac{1}{x - 1} = \frac{7}{5} \\ \frac{1}{2 y - 1} = \frac{3}{5} \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{19}{7} \\ y = \frac{4}{3} \end{cases}$

Câu 11:

Giải hệ phương trình sau:

\{\begin{cases} \frac{1}{2 x + y} + \frac{1}{x - 2 y} = \frac{5}{8} \\ \frac{1}{2 y + 1} - \frac{1}{x - 2 y} = - \frac{3}{8} \end{cases}

Xem đáp án

$\{\begin{cases} \frac{1}{2 x + y} + \frac{1}{x - y} = \frac{5}{8} \\ \frac{1}{2 y + 1} - \frac{1}{x - 2 y} = - \frac{3}{8} \end{cases}$

Đặt $a = \frac{1}{2 x + y} b = \frac{1}{x - 2 y}$ hệ phương trình thành:

$\{\begin{cases} a + b = \frac{5}{8} \\ a - b = \frac{- 3}{8} \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{1}{8} \\ b = \frac{1}{2} \end{cases} \Rightarrow \{\begin{cases} \frac{1}{2 x + y} = \frac{1}{8} \\ x - 2 y = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{18}{5} \\ y = \frac{4}{5} \end{cases}$

Câu 12:

Giải hệ phương trình sau:

$\{\begin{cases} 3 \sqrt{x - 1} + 2 \sqrt{y} = 13 \\ 2 \sqrt{x - 1} - \sqrt{y} = 4 \end{cases}$

Xem đáp án

$\{\begin{cases} 3 \sqrt{x - 1} + 2 \sqrt{y} = 13 \\ 2 \sqrt{x - 1} - \sqrt{y} = 4 \end{cases}$

Đặt $t = \sqrt{x - 1} (x \geq 1)$ . $u = \sqrt{y} (y \geq 0)$ , hệ phương trình thành:

$\{\begin{cases} 3 t + 2 u = 13 \\ 2 t - u = 4 \end{cases} \Leftrightarrow \{\begin{cases} t = 3 \\ u = 2 \end{cases} \Leftrightarrow \{\begin{cases} \sqrt{x - 1} = 3 \\ \sqrt{y} = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 10 \\ y = 4 \end{cases}$

Câu 13:

Giải hệ phương trình sau:

\{\begin{cases} |x - 1| + |y + 2| = 2 \\ 4 |x - 1| + 3 |y + 2| = 7 \end{cases}

Xem đáp án

$\{\begin{cases} |x - 1| + |y + 2| = 2 \\ 4 |x - 1| + 3 |y + 2| = 7 \end{cases} \Leftrightarrow \{\begin{cases} |x - 1| = 1 \\ |y + 2| = 1 \end{cases} \Leftrightarrow \{\begin{cases} [\begin{array}{l} x - 1 = 1 \\ x - 1 = - 1 \end{array} \\ [\begin{array}{l} y + 2 = 1 \\ y + 2 = - 1 \end{array} \end{cases} \Leftrightarrow \{\begin{cases} [\begin{array}{l} x = 2 \\ x = 0 \end{array} \\ [\begin{array}{l} y = - 1 \\ y = - 3 \end{array} \end{cases} \Rightarrow (x; y) \in \{(2; - 1); (2; - 3); (0; - 1); (0; - 3)\}$

Câu 14:

Biết rằng Đa thức P(x) chia hết cho x - a khi và chỉ khi P(a) = 0. Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho $x + 1; x - 3$ , biết:

$P (x) = m x^{3} + (m - 2) x^{2} - (3 n - 5) x - 4 n$

Xem đáp án

Vì $P (x) ⋮ (x + 1); (x - 3) \Rightarrow \{\begin{cases} P (- 1) = 0 \\ P (3) = 0 \end{cases}$

$\Rightarrow \{\begin{cases} - m + m - 2 + 3 n - 5 - 4 n \\ 27 m + 9 m - 18 - 9 n + 15 - 4 n = 0 \end{cases} \Leftrightarrow \{\begin{cases} m = - \frac{22}{9} \\ m = - 7 \end{cases}$

Câu 15:

Giải hệ phương trình bằng phương pháp thế:

$\{\begin{cases} x - y = 3 \\ 3 x - 4 y = 2 \end{cases}$

Xem đáp án

$\{\begin{cases} x - y = 3 \\ 3 x - 4 y = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 + y \\ 3 (3 + y) - 4 y = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 10 \\ y = 7 \end{cases}$

Câu 16:

Giải hệ phương trình bằng phương pháp thế:

$\{\begin{cases} 7 x - 3 y = 5 \\ 4 x + y = 2 \end{cases}$

Xem đáp án

$\{\begin{cases} 7 x - 3 y = 5 \\ 4 x + y = 2 \end{cases} \Leftrightarrow \{\begin{cases} 7 x - 3 (2 - 4 x) = 5 \\ y = 2 - 4 x \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{11}{19} \\ y = \frac{- 6}{19} \end{cases}$

Câu 17:

Giải hệ phương trình bằng phương pháp thế:

$\{\begin{cases} x + 3 y = - 2 \\ 5 x - 4 y = 11 \end{cases}$

Xem đáp án

$\{\begin{cases} x + 3 y = - 2 \\ 5 x - 4 y = 11 \end{cases} \Leftrightarrow \{\begin{cases} x = - 2 - 3 y \\ 5 (- 2 - 3 y) - 4 y = 11 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{25}{19} \\ y = \frac{- 21}{19} \end{cases}$

Câu 18:

Cho tam giác đều ABC. Vẽ đường tròn (I) đường kính BC cắt cạnh AB, AC lần lượt tại D và E

a) Tính số đo mỗi cung BD (cung lớn và cung nhỏ)

b) Chứng tỏ rằng $\overset{⏜}{B D} = \overset{⏜}{D E} = \overset{⏜}{E C}$

Xem đáp án

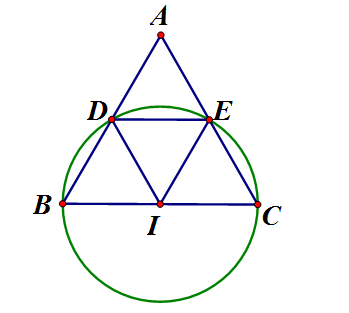
Cho tam giác đều ABC. Vẽ đường tròn (I) đường kính BC cắt cạnh AB, AC (ảnh 1)

a) Ta có: IB = ID = R và $∠ B = 60^{0} \Rightarrow Δ B D I$ đều nên sđ BD nhỏ $= 60^{0}$ nên số đo cung BC lớn $= 360^{0} - 60^{0} = 300^{0}$

b) Chứng minh tương tự $\Rightarrow Δ I E C$ đều nên sđ cung EC $= 60^{0}$

$s d \overset{⏜}{D E} = 180^{0} - (s d \overset{⏜}{B D} + s d \overset{⏜}{E C}) = 180^{0} - {2.60}^{0} = 60^{0}$

$\Rightarrow s d \overset{⏜}{B D} = s d \overset{⏜}{D E} = s d \overset{⏜}{E C} = 60^{0} \Rightarrow \overset{⏜}{B D} = \overset{⏜}{D E} = \overset{⏜}{E C}$

Câu 19:

Cho đường tròn (O; R), các dây AB, CD, EF có độ dài như sau $: A B = R, C D = R \sqrt{2}$ , $E F = R \sqrt{3} .$ Tính số đo các cung $\overset{⏜}{A B}, \overset{⏜}{C D}, \overset{⏜}{E F}$

Xem đáp án

Vì $A B = R \Rightarrow Δ O A B$ đều $\Rightarrow s d \overset{⏜}{A B} = 60^{0}$

Ta có: $O C^{2} + O D^{2} = 2 R^{2} = C D^{2} \Rightarrow Δ O C D$ vuông cân tại O nên $s d \overset{⏜}{C D} = 90^{0}$

$E F = R \sqrt{3} \Rightarrow s d \overset{⏜}{E F} = 120^{0}$

Câu 20:

Cho đường tròn (O) đường kính AB, vẽ góc ở tâm $∠ A O C = 50^{0}$ với C nằm trên (O). Vẽ dây CD vuông góc với AB và dây DE song song với AB

a) Tính số đo cung nhỏ $\overset{⏜}{B E}$

b) Tính số đo cung $\overset{⏜}{C B E} .$ Từ đó suy ra 3 điểm C, O, E thẳng hàng.

Xem đáp án

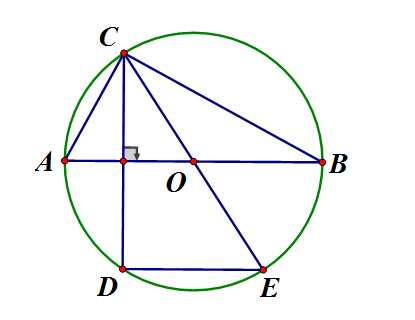
Cho đường tròn (O) đường kính AB, vẽ góc AOC = 50 độ ở tâm với C (ảnh 1)

a) $∠ A O C = 50^{0} \Rightarrow ∠ C A B = \frac{180^{0} - 50^{0}}{2} = 65^{0} \Rightarrow s d \overset{⏜}{C B} = 130^{0}$ (tính chất tứ giác nội tiếp)

$\Rightarrow s d \overset{⏜}{A C} = 50^{0} \Rightarrow s d \overset{⏜}{A D} = 50^{0}$ mà $A B / / D E \Rightarrow s d \overset{⏜}{B D} = 50^{0}$

b) Ta có: $D E / / A B \Rightarrow ∠ D = 90^{0}$ , mà góc D là góc nội tiếp nên CE là đường kính

$\Rightarrow C, O, E$ thẳng hàng.

Câu 21:

Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = 2R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm)

a) Tính $∠ A O M$

b) Tính $∠ A O B$ và số đo cung AB nhỏ .

Xem đáp án

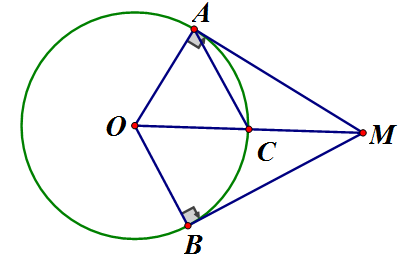
Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = 2R. Từ M (ảnh 1)

a) Gọi $O M \cap (O) = C$

$Δ O A M$ vuông tại A nên $\cos O = \frac{O A}{O M} = \frac{1}{2} \Rightarrow ∠ O = 60^{0} \Rightarrow ∠ A O M = 60^{0}$

b) Theo tính chất tiếp tuyến ta có: OM là phân giác $∠ A O B$

$\Rightarrow ∠ A O B = 2 ∠ A O M = 120^{0} \Rightarrow s d \overset{⏜}{A B} = 60^{0}$

Câu 22:

Cho tam giác ABC cân tại A. Vẽ đường tròn tâm O, đường kính BC. Đường tròn (O) cắt AB, AC lần lượt tại M, N

a) Chứng minh $s d \overset{⏜}{B M} = s d \overset{⏜}{C N}$

b) Tính $∠ M O N,$ biết $∠ B A C = 40^{0}$

Xem đáp án

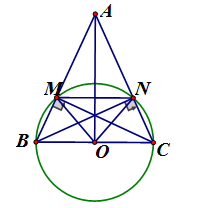
Cho tam giác ABC cân tại A. Vẽ đường tròn tâm O, đường kính BC. Đường tròn (ảnh 1)

a) Nối $C M, B N \Rightarrow ∠ B M C = ∠ B N C = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)

Xét $Δ B M C, Δ B N C$ có: $∠ B = ∠ C, B C c h u n g$

$\Rightarrow Δ B M C = Δ B N C (c h - g n) \Rightarrow B M = C N$ $\Rightarrow s d \overset{⏜}{B M} = s d \overset{⏜}{C N}$

b) $∠ A = 40^{0} \Rightarrow ∠ A B C = ∠ A C B = \frac{180^{0} - 40^{0}}{2} = 70^{0}$ $\Rightarrow ∠ M_{1} = ∠ N_{1} = 70^{0}$ (tính chất tam giác cân)

$\begin{array}{l} \Rightarrow ∠ O_{1} = ∠ O_{2} = 180^{0} - (∠ B + ∠ M_{1}) = 40^{0} \\ \Rightarrow ∠ M O N = 180^{0} - {2.40}^{0} = 100^{0} \end{array}$

Câu 23:

Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa A vẽ nửa đường tròn đường kính BC. D là điểm trên nửa đường tròn sao cho $s d \overset{⏜}{C D} = 60^{0} .$ Gọi M là giao điểm của AD và BC. Chứng minh rằng BM = 2MC.

Xem đáp án

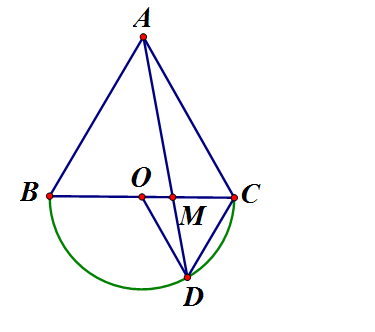
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa A vẽ nửa đường (ảnh 1)

Gọi O là trung điểm BC

Ta có O là tâm của nửa đường tròn đường kính BC $\Rightarrow O C = O D = R$

Mà $s d \overset{⏜}{C O D} = s d \overset{⏜}{C D} = 60^{0} \Rightarrow Δ C O D$ đều $\Rightarrow O C = O D$ mà $∠ O C D = 60^{0} \Rightarrow O C = O D$

Vậy $\frac{A B}{C D} = \frac{B C}{O C} = 2$

Ta có $∠ B = ∠ O C D = 60^{0}$ mà ở vị trí so le trong nên AB // CD

Áp dụng đinh lý Ta let $\Rightarrow \frac{B M}{M C} = \frac{A M}{M D} = \frac{A B}{C D} = 2 \Rightarrow B M = 2 M C$