5 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 34 - Đề 1

Bài tập theo tuần Toán 9 - Tuần 34

Bài tập theo tuần Toán 9 - Tuần 34 - Đề 1

472 lượt thi
5 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giải phương trình $2 x^{2} - 5 x - 3 = 0$

Xem đáp án

$2 x^{2} - 5 x - 3 = 0 Δ = {(- 5)}^{2} - 4.2. (- 3) = 49 \Rightarrow \sqrt{Δ} = 7$

Suy ra phương trình có hai nghiệm

[\begin{array}{l} x_{1} = \frac{5 + 7}{4} = 3 \\ x_{2} = \frac{5 - 7}{4} = - \frac{1}{2} \end{array} S = \{3; \frac{- 1}{2}\}

Câu 2:

Giải hệ phương trình

\{\begin{cases} 2 x - y = - 1 \\ 3 x + 2 y = 9 \end{cases}

Xem đáp án

$\{\begin{cases} 2 x - y = - 1 \\ 3 x + 2 y = 9 \end{cases} \Leftrightarrow \{\begin{cases} 4 x - 2 y = - 2 \\ 3 x + 2 y = 9 \end{cases} \Leftrightarrow \{\begin{cases} 7 x = 7 \\ y = 2 x + 1 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 3 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất

(x; y) = (1; 3)

Câu 3:

Cho hàm số $y = \frac{1}{2} x^{2}$ có đồ thị (P).

a) Vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy.

b) Tìm tọa độ giao điểm của đồ thị (P) và đồ thị hàm số y = x + 4

Xem đáp án

a) Học sinh tự vẽ

b) Ta có phương trình hoành độ giao điểm của (P) và (d) là

$\begin{array}{l} \frac{1}{2} x^{2} = x + 4 \Leftrightarrow x^{2} - 2 x - 8 = 0 \\ Δ' = - (- 8) = 9 \\ \Rightarrow [\begin{array}{l} x_{1} = 1 + \sqrt{9} = 4 \Rightarrow y_{1} = 8 \\ x_{2} = 1 - \sqrt{9} = - 2 \Rightarrow y_{2} = 2 \end{array} \end{array}$

Vậy tọa độ (P) và (d) là : $A (4; 8) B (- 2; 2)$

Câu 4:

Cho phương trình $x^{2} - 2 (m + 1) x + m - 4 = 0$ (ẩn số là x)

a) Tính $Δ'$

b) Gọi $x_{1}, x_{2}$ là hai nghiệm của phương trình. Chứng minh rằng biểu thức $A = x_{1} (1 - x_{2}) + x_{2} (1 - x_{1})$ không phụ thuộc vào m.

Xem đáp án

$\begin{array}{l} x^{2} - 2 (m + 1) x + m - 4 = 0 \\ Δ' = {(m + 1)}^{2} - (m - 4) = m^{2} + m + 5 > 0 \end{array}$

b) Khi

Δ > 0

áp dụng hệ thức Vi et ta có

\{\begin{cases} x_{1} + x_{2} = 2 m + 2 \\ x_{1} x_{2} = m - 4 \end{cases}

A = x_{1} (1 - x_{2}) + x_{2} (1 - x_{1}) = x_{1} + x_{2} - 2 x_{1} x_{2} = 2 m + 2 - 2 m + 8 = 10

Vậy A không phụ thuộc vào m.

Câu 5:

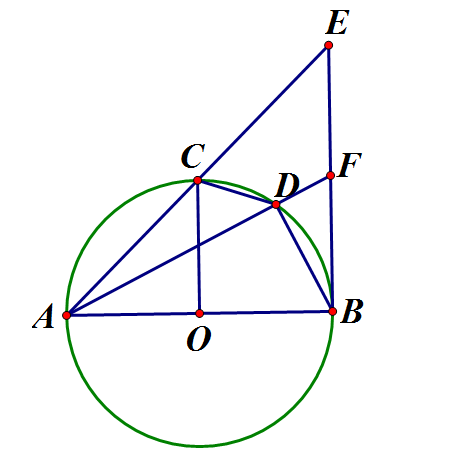
Cho nửa đường tròn (O), đường kính AB. Kẻ tiếp tuyến Bx với nửa đường tròn. Gọi C là điểm trên nửa đường tròn sao cho cung CA bằng cung CB, D là điểm tùy ý trên cung CB (D khác C và B), các tia AC và AD cắt tia Bx theo thứ tự ở E và F

a) Tính số đo góc AEB

b) Chứng minh tứ giác CDFE nội tiếp được đường tròn

c) Chứng minh $B E^{2} = A D . A F$

Xem đáp án

Cho nửa đường tròn (O), đường kính AB. Kẻ tiếp tuyến Bx với nửa đường tròn (ảnh 1)

s d \overset{⏜}{A C} = s d \overset{⏜}{C B} \Rightarrow \hat{A C B} = 45^{0}

mà

Δ A B E

vuông tại B (do BE là tiếp tuyến)

\Rightarrow \hat{A E B} = 45^{0}

b) Ta có $\hat{A E B} = 45^{0}$ mà $\hat{C D A} = \frac{1}{2} s d \overset{⏜}{A C} = \frac{1}{2} {.90}^{0} = 45^{0}$ (do C chính giữa cung AB)

$\Rightarrow \hat{A E B} = \hat{C D A} = 45^{0} \Rightarrow C D F E$ là tứ giác nội tiếp

c) Ta có $\hat{A D B} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn )

$\Rightarrow Δ A B F$ vuông tại B, BD là đường cao $\Rightarrow A D . A F = A B^{2}$

Mà AB = BE (do tam giác ABE vuông cân) $\Rightarrow B E^{2} = A D . A F (d p c m)$

Bắt đầu thi ngay