7 câu hỏi trắc nghiệm thuộc Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 7)

Câu 1:

Giải các phương trình và hệ phương trình sau:

$x^{2} + x - 6 = 0$

Δ = 25 > 0

phương trình có hai nghiệm phân biệt

x_{1} = \frac{- 1 + 5}{2} = 2; x_{2} = \frac{- 1 - 5}{2} = - 3

Tập nghiệm phương trình là S = {2;-3}

Câu 2:

Giải các phương trình và hệ phương trình sau:

$x - 3 \sqrt{x} = 4$

Xem đáp án

Giải phương trình $x - 3 \sqrt{x} = 4$ .

Đặt $t = \sqrt{x} (x \geq 0, t \geq 0)$ phương trình trở thành $t^{2} - 3 t - 4 = 0$ .

Ta có $1 - (- 3) - 4 = 0$ nên phương trình có hai nghiệm $t_{1} = - 1$ (loại), $t_{2} = 4$ (nhận).

Với $t = 4 \Rightarrow \sqrt{x} = 4 \Leftrightarrow x = 16$ .

Tập nghiệm phương trình là S = {16}.

Câu 3:

Giải các phương trình và hệ phương trình sau: $\{\begin{cases} x - y = - 1 \\ 2 x + 3 y = 8 \end{cases}$

Xem đáp án

Giải hệ phương trình $\{\begin{cases} x - y = - 1 \\ 2 x + 3 y = 8 \end{cases}$

$\{\begin{cases} x - y = - 1 \\ 2 x + 3 y = 8 \end{cases} \Leftrightarrow \{\begin{cases} 3 x - 3 y = - 3 \\ 2 x + 3 y = 8 \end{cases} \Leftrightarrow \{\begin{cases} 5 x = 5 \\ 2 x + 3 y = 8 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ 3 y = 8 - 2.1 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 2 \end{cases}$

Tập nghiệm hệ phương trình là $S = \{(1; 2)\}$ .

Câu 4:

Cho Parabol $(P) : y = - 0, 5 x^{2}$ và đường thẳng (d): y = -0,5x + 2.

1) Vẽ đồ thị của hàm số $y = - 0, 5 x^{2}$ .

2) Viết phương trình đường thẳng $(d_{1})$ biết $(d_{1})$ vuông góc với (d) và $(d_{1})$ tiếp xúc (P)

Xem đáp án

1) Vẽ đồ thị của hàm số y = -0,5x²

Cho Parabol p y -0,5x 2 và đường thẳng (d) y = -0,5x + 2. 1) Vẽ đồ thị của hàm sốp y -0,5x 2 (ảnh 1)

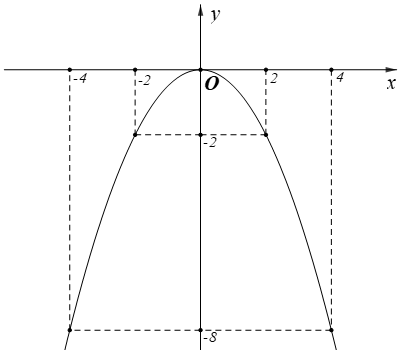
Cho Parabol p y -0,5x 2 và đường thẳng (d) y = -0,5x + 2. 1) Vẽ đồ thị của hàm sốp y -0,5x 2 (ảnh 2)

2) $(d_{1}) : y = a x + b$ vuông góc với $(d) : y = - 0, 5 x + 2$ nên có $a . (- 0, 5) = - 1 \Leftrightarrow a = 2$ .

$(d_{1}) : y = 2 x + b$ tiếp xúc $(P) : y = - 0, 5 x^{2}$ nên phương trình $- 0, 5 x^{2} = 2 x + b \Leftrightarrow - 0, 5 x^{2} - 2 x - b = 0$ có nghiệm kép nên $Δ = 4 - 2 b = 0 \Leftrightarrow b = 2$ .

Vậy phương trình đường thẳng $(d_{1}) : y = 2 x + 2$ .

Câu 5:

Cho phương trình: $x^{2} - 2 (m + 1) x + m^{2} + m = 0$ với m là tham số.

1) Tìm các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x₁ , x₂

2) Tìm hệ thức liên hệ giữa x₂ và x₂ mà không phụ thuộc vào tham số m.

$\Leftrightarrow m^{2} + 2 m + 1 - m^{2} - m = m + 1 > 0 \Leftrightarrow m > - 1$

Xem đáp án

Phương trình $x^{2} - 2 (m + 1) x + m^{2} + m = 0$ (1)

1) Phương trình (1) có hai nghiệm phân biệt khi $Δ^{'} > 0 \Leftrightarrow {[- (m + 1)]}^{2} - 1. (m^{2} + m) > 0$ .

Vậy m > -1 thì phương trình (1) có hai nghiệm phân biệt.

2) Theo hệ thức Viet ta có: $\{\begin{cases} x_{1} + x_{2} = 2 (m + 1) \\ x_{1} . x_{2} = m^{2} + m \end{cases}$

$\Leftrightarrow \{\begin{cases} m = \frac{x_{1} + x_{2}}{2} - 1 \\ x_{1} x_{2} = {(\frac{x_{1} + x_{2}}{2} - 1)}^{2} + \frac{x_{1} + x_{2}}{2} - 1 \end{cases}$

=> ${(x_{1} + x_{2})}^{2} - 2 (x_{1} + x_{2}) - 4 x_{1} x_{2} = 0$ là hệ thức liên hệ giữa x₁ và x₂ mà không phụ thuộc vào tham số m.

Câu 6:

Bác Tư đến siêu thị mua một cái quạt máy và một ấm đun siêu tốc với tổng số tiền theo giá niêm yết là 630 000 đồng. Tuy nhiên, trong tuần lễ tri ân khách hàng nên siêu thị đã giảm giá quạt máy 15% và giảm giá ấm đun siêu tốc 12% so với giá niêm yết của từng sản phẩm. Nên Bác Tư chỉ phải trả 543 000 đồng khi mua hai sản phẩm trên. Hỏi giá niêm yết (khi chưa giảm giá) của một cái quạt máy và một ấm đun siêu tốc là bao nhiêu?

Xem đáp án

Gọi giá tiền niêm yết (khi chưa giảm giá) của một cái quạt máy và một ấm đun siêu tốc là x; y (x > 0, y > 0) (đồng).

Tổng số tiền mua 2 sản phẩm theo giá niêm yết là 630 000 đồng nên ta có phương trình:

x + y = 630 000.

Giá tiền quạt máy sau khi giảm giá là $x - 15 % x = 85 % x = 0, 85 x$ .

Giá tiền ấm siêu tốc sau khi giảm giá là $y - 12 % y = 88 % y = 0, 88 y$ .

Do bác Tư phải trả 543 000 đồng khi mua hai sản phẩm nên ta có phương trình

$0, 85 x + 0, 88 y = 543 000 (2)$ .

Từ (1) và (2) ta có hệ phương trình: $\{\begin{cases} x + y = 630 000 \\ 0, 85 x + 0, 88 y = 543 000 \end{cases}$

$\Leftrightarrow \{\begin{cases} 0, 88 x + 0, 88 y = 554 400 \\ 0, 85 x + 0, 88 y = 543 000 \end{cases} \Leftrightarrow \{\begin{cases} 0, 03 x = 11 400 \\ x + y = 630 000 \end{cases}$

$\Leftrightarrow \{\begin{cases} x = 380 000 \\ 380 000 + y = 630 000 \end{cases} \Leftrightarrow \{\begin{cases} x = 380 000 \\ y = 250 000 \end{cases}$ (thỏa mãn)

Vậy giá tiền niêm yết (khi chưa giảm giá) của một cái quạt máy và một ấm đun siêu tốc lần lượt là 380 000 đồng và 250 000 đồng.

Câu 7:

Cho đường tròn tâm O đường kính AB và một điểm C tùy ý trên (O) (C khác A, B và AC < CB). Các tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại D. Dựng CH vuông góc với BD tại H (H nằm trên BD). Đường thẳng DO cắt CH và CB lần lượt tại M và N.

1) Chứng minh tứ giác CNHD nội tiếp được trong đường tròn.

2) Chứng minh CM = CO.

3) Các đường thẳng AB và CD cắt nhau tại E. Chứng minh EA.EB = EC².

4) Khi quay tam giác DNB một vòng quanh cạnh DN ta được một hình nón. Biết OB = 6cm, BD = 8cm. Tính thể tích của hình nón tạo thành.

Xem đáp án

1) Ta có $C H ⊥ B D$ nên H nhìn CD dưới một góc vuông (1)

Theo tính chất hai tiếp tuyến cắt nhau CD và BD, ta có DC = DB

Hai bán kính OC = OB

=> OD là trung trực của BC $\Rightarrow O D ⊥ C B$

=> N nhìn CD dưới một góc vuông (2)

Từ (1) và (2) suy ra tứ giác CNHD nội tiếp được trong đường tròn.

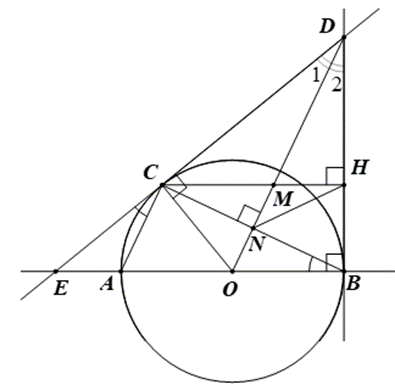
Cho đường tròn tâm O đường kính AB và một điểm C tùy ý trên (O) (C khác A, B và AC < CB). Các tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại D. (ảnh 1)

2) Theo tính chất hai tiếp tuyến cắt nhau CD và BD, ta có DC = DB, ta có $\hat{D_{1}} = \hat{D_{2}}$

Theo tính chất tiếp tuyến và giả thiết, ta có góc $\hat{C O D} = \hat{D M H}$ (cùng phụ với hai góc bằng nhau $\hat{D_{1}} = \hat{D_{2}}$ )

Mặt khác $\hat{D M H} = \hat{C M O}$ (đối đỉnh) => $\hat{C O D} = \hat{C M O}$

$Δ C O M$ có $\hat{C O M} = \hat{C M O}$

$\Rightarrow Δ C O M$ cân tại C => CM = CO

3) Xét $Δ E A C$ và $Δ E C B$ có góc E chung và góc $\hat{E C A} = \hat{C B A}$ (cùng chắn cung AC)

$\Rightarrow Δ E A C ∽ Δ E C B (g . g) \Rightarrow \frac{E A}{E C} = \frac{E C}{E B} \Rightarrow E A . E B = E C^{2}$

4) Hình nón được tạo bởi tam giác vuông DNB quay quanh DN

Suy ra bán kính r = NB và chiều cao h = ND.

Theo Pythagore cho tam giác vuông BOD vuông tại D có:

$O D = \sqrt{O B^{2} + B D^{2}} = \sqrt{36 + 64} = 10 (cm)$ .

Theo hệ thức lượng trong tam giác vuông BOD, ta có:

$B N \cdot O D = O B \cdot B D \Rightarrow B N = \frac{6 \cdot 8}{10} = 4, 8 (cm)$ .

Và $B D^{2} = D N \cdot D O \Rightarrow D N = \frac{64}{10} = 6, 4 (cm)$

Thể tích của hình nón tạo thành

$V = \frac{1}{3} π \cdot r^{2} \cdot h = \frac{1}{3} π . {(4, 8)}^{2} \cdot 6, 4 = \frac{6144}{125} π \approx 154, 4156 ({cm}^{3})$ .