20 câu hỏi trắc nghiệm thuộc Dạng 1: Hàm số bậc nhất có đáp án

Câu 1:

Cho hàm số $y = f (x) = 2 x + 3$

a) Tính giá trị của hàm số khi $x = - 2; - 0, 5; 0; 3; \frac{\sqrt{3}}{2}$

Xem đáp án

a) Ta có: Khi $x = - 2 \Rightarrow f (- 2) = 2. (- 2) + 3 = - 4 + 3 = - 1$

$x = - \frac{1}{2} \Rightarrow f (- \frac{1}{2}) = 2. (- \frac{1}{2}) + 3 = - 1 + 3 = 2$

$x = 0 \Rightarrow f (0) = 2.0 + 3 = 3$

$x = 3 \Rightarrow f (3) = 2.3 + 3 = 6 + 3 = 9$

$x = \frac{\sqrt{3}}{2} \Rightarrow f (\frac{\sqrt{3}}{2}) = 2. \frac{\sqrt{3}}{2} + 3 = \sqrt{3} + 3$

Câu 2:

b) Tìm giá trị của x để hàm số có giá trị bằng 10 , -7

Xem đáp án

b) +) Để hàm số $y = f (x) = 2x + 3$ có giá trị bằng 10 $\Rightarrow 2x + 3=10$

$\Rightarrow 2 x = 10 - 3 \Rightarrow 2 x = 7 \Rightarrow x = \frac{7}{2}$

Vậy khi $x = \frac{7}{2}$ thì hàm số có giá trị bằng 10.

+) Để hàm số $y = f (x) = 2x + 3$ có giá trị bằng -7 $\Rightarrow 2 x + 3 = - 7$

$\Rightarrow 2 x = - 7 - 3 \Rightarrow 2 x = - 10 \Rightarrow x = - 5$

Vậy khi x=-5 thì hàm số có giá trị bằng -7.

Câu 3:

Cho các hàm số: $y = 2 m x + m + 1 (1)$ và $y = (m - 1) x + 3 (2)$

a) Xác định m để hàm số (1) đồng biến, còn hàm số (2) nghịch biến.

Xem đáp án

a) Hàm số (1) đồng biến và hàm số (2) nghịch biến:

$\Leftrightarrow \{\begin{matrix} 2 m > 0 \\ m - 1 < 0 \end{matrix} \Leftrightarrow \{\begin{matrix} m > 0 \\ m < 1 \end{matrix} \Leftrightarrow 0 < m < 1.$

Câu 4:

b) Xác định m để đồ thị của hàm số song song với nhau.

Xem đáp án

b) Đồ thị của hai hàm số song song với nhau:

$\Leftrightarrow \{\begin{matrix} 2 m = m - 1 \\ m + 1 \neq 3 \end{matrix} \Leftrightarrow \{\begin{matrix} m = - 1 \\ m < 1 \end{matrix} \Leftrightarrow m = - 1.$

Câu 5:

c) Chứng minh rằng đồ thị (d) của hàm số (1) luôn đi qua một điểm cố định với mọi giá trị của m

Xem đáp án

c) Viết lại hàm số (1) dưới dạng $y = m (2 x + 1) + 1.$

Ta thấy với mọi giá trị của m khi $x = - \frac{1}{2}$ thì y=1

Vậy đồ thị (d) của hàm số (1) luôn đi qua một điểm cố định là điểm $M (- \frac{1}{2}; 1) .$

Câu 6:

Cho hàm số $y = (m - 3) x + m + 2$ (*)

a) Tìm m để đồ thị hàm số (*) cắt trục tung tại điểm có tung độ bằng -3.

Xem đáp án

a) Để đồ thị hàm số $y = (m - 3) x + m + 2$ cắt trục tung tại điểm có tung độ bằng – 3 $\Rightarrow$ x = 0; y = - 3

Ta có: $- 3 = (m - 3) .0 + m + 2$

$\Leftrightarrow m + 2 = - 3$

$\Leftrightarrow m = - 5$

Vậy với m=-5 thì đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -3

Câu 7:

c) Tìm m để đồ thị hàm số (*) vuông góc với đường thẳng y=2x-3

Xem đáp án

c) Để đồ thị hàm số $y = (m - 3) x + m + 2$ vuông góc với đường thẳng $y = 2 x - 3$

$\Leftrightarrow a . a ’ = - 1 \Leftrightarrow (m - 3) .2 = - 1$

$\Leftrightarrow 2 m - 6 = - 1 \Leftrightarrow 2 m = 5 \Leftrightarrow m = \frac{5}{2}$

Vậy với $m = \frac{5}{2}$ đồ thị hàm số $y = (m - 3) x + m + 2$ vuông góc với đường thẳng $y = 2 x - 3$

Câu 8:

Trong hệ trục toạ độ Oxy cho hàm số y=2x+m (*) 1) Tìm giá trị của m để đồ thị hàm số đi qua:

a,

A (- 1; 3)

Xem đáp án

1) a) Để đồ thị hàm số $y = 2 x + m$ đi qua: $A (- 1; 3)$

$\Leftrightarrow 3 = 2. (- 1) + m$

$\Leftrightarrow 3 = - 2 + m$

$\Leftrightarrow m = 5$

Vậy với m=5 thì đồ thị hàm số $y = 2 x + m$ đi qua: $A (- 1; 3)$

Câu 9:

1) Tìm giá trị của m để đồ thị hàm số đi qua:

b, $B (\sqrt{2}; - 5 \sqrt{2})$

Xem đáp án

b) Để đồ thị hàm số $y = 2 x + m$ đi qua: $B (\sqrt{2}; - 5 \sqrt{2})$

$\Leftrightarrow - 5 \sqrt{2} = 2. \sqrt{2} + m$

$\Leftrightarrow m = - 7 \sqrt{2}$

Vậy với $m = - 7 \sqrt{2}$ thì đồ thị hàm $y = 2 x + m$ đi qua: $B (\sqrt{2}; - 5 \sqrt{2})$

Câu 10:

2) Tìm m để đồ thị hàm số (*) cắt đồ thị hàm số $y = 3 x - 2$ trong góc phần tư thứ IV

Xem đáp án

2) Toạ độ giao điểm của đồ thị hàm số với $y = 2 x + m$ đồ thị hàm số $y = 3 x - 2$ là nghiệm của hệ phương trình

$\{\begin{cases} y = 2x + m \\ y = 3x - 2 \end{cases} \Leftrightarrow \{\begin{cases} 3x - 2 = 2x + m \\ y = 3x - 2 \end{cases} \Leftrightarrow \{\begin{cases} 3x - 2x = m + 2 \\ y = 3x - 2 \end{cases}$

$\Leftrightarrow \{\begin{cases} x = m + 2 \\ y = 3. (m + 2) - 2 \end{cases} \Leftrightarrow \{\begin{cases} x = m + 2 \\ y = 3m + 6 - 2 \end{cases} \Leftrightarrow \{\begin{cases} x = m+ 2 \\ y = 3m +4 \end{cases}$

Vậy toạ độ giao điểm của đồ thị hàm số $y = 2 x + m$ với đồ thị hàm số $y = 3 x - 2$ là $(m+ 2 ; 3m +4)$

Để đồ thị hàm số cắt đồ thị hàm số y= 3x -2 trong góc phần tư thứ IV thì :

$\{\begin{cases} x > 0 \\ y < 0 \end{cases} \Leftrightarrow \{\begin{cases} m + 2 > 0 \\ 3m + 4 < 0 \end{cases} \Leftrightarrow \{\begin{cases} m > - 2 \\ m < - \frac{4}{3} \end{cases} \Leftrightarrow - 2 < m < - \frac{4}{3}$

Vậy với $- 2 < m < - \frac{4}{3}$ thì đồ thị hàm số $y = 2 x + m$ cắt đồ thị hàm số $y = 3 x - 2$ trong góc phần tư thứ IV

Câu 11:

Cho hàm số $y = (2 m + 1) x + m + 4$ (m là tham số) có đồ thị là đường thẳng (d).

a) Tìm m để (d) đi qua điểm $A (- 1; 2)$ .

Xem đáp án

a) Ta có (d) đi qua điểm

$A (- 1; 2) \Leftrightarrow \Leftrightarrow 2 = (2 m + 1) (- 1) + m + 4 \Leftrightarrow \Leftrightarrow 2 = - m + 3 \Leftrightarrow m = 1.$ .

Câu 12:

b) Tìm m để (d) song song với đường thẳng (Δ) có phương trình: $y = 5 x + 1$ .

Xem đáp án

b) Ta có

(d) // (Δ) \Leftrightarrow \{\begin{cases} 2 m + 1 = 5 \\ m + 4 \neq 1 \end{cases} \Leftrightarrow \Leftrightarrow m = 2

Câu 13:

c) Chứng minh rằng khi m thay đổi thì đường thẳng (d) luôn đi qua một điểm cố định.

Xem đáp án

c) Giả sử $M (x_{0}; y_{0})$ là điểm cố định của đường thẳng (d).

Khi đó ta có: $y_{0} = (2 m + 1) x_{0} + m + 4 \forall m \Leftrightarrow (2 x_{0} + 1) m + x_{0} - y_{0} + 4 = 0 \forall m$

$\Leftrightarrow \{\begin{cases} 2 x_{0} + 1 = 0 \\ x_{0} - y_{0} + 4 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x_{0} = - \frac{1}{2} \\ y_{0} = \frac{7}{2} \end{cases}$

Vậy khi m thay đổi đường thẳng (d) luôn đi qua điểm cố định $M (- \frac{1}{2}; \frac{7}{2})$

Câu 14:

Tìm giá trị của tham số để đường thẳng $d_{1} : y = - x + 2$ cắt đường thẳng $d_{2} : y = 2 x + 3 - k$ tại một điểm nằm trên trục hoành.

Xem đáp án

Ta thấy hai đường thẳng $d_{1}; d_{2}$ luôn cắt nhau (vì $- 1 \neq 2$ )

+ Đường thẳng $d_{1}$ cắt trục hoành tại điểm $A (2; 0)$

+ Đường thẳng $d_{2}$ cắt trục hoành tại điểm $B (\frac{k - 3}{2}; 0)$

+ Để hai đường thẳng cắt nhau tại một điểm trên trục hoành thì $\frac{k - 3}{2} = 2 \Leftrightarrow k = 7$ .

Câu 15:

Cho hai đường thẳng( $d_{1}$ ) : $y = 2 x + 5$ ; $(d_{2}) : y = - 4 x + 1$ cắt nhau tại I. Tìm để đường thẳng $(d_{3}) : y = (m + 1) x + 2 m - 1$ đi qua điểm ?

Xem đáp án

Tọa độ là nghiệm của hệ $\{\begin{cases} y = 2 x + 5 \\ y = - 4 x + 1 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{- 2}{3} \\ y = \frac{11}{3} \end{cases}$

Do $(d_{3})$ đi qua điểm nên $\frac{11}{3} = \frac{- 2}{3} (m + 1) + 2 m - 1 \Leftrightarrow m = 4$ .

Vậy m=4 là giá trị cần tìm.

Câu 16:

Xác định hàm số $y = a x + b,$ biết đồ thị (d) của nó đi qua $A (2; 1, 5)$ và $B (8; - 3) .$ Khi đó hãy tính:

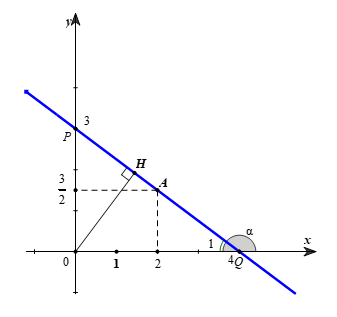
a) Vẽ đồ thị hàm số (d) vừa tìm được và tính góc $α$ tạo bởi đường thẳng (d) và trục Ox;

Xem đáp án

Vì (d) đi qua $A (2; 1, 5)$ và $B (8; - 3)$ nên toạ độ của A và B phải thoả mãn phương trình $y = a x + b .$

Thay $x = 2; y = 1, 5$ rồi lại thay $x = 8; y = - 3$ vào phương trình $y = a x + b$ ta được hệ phương trình: $\{\begin{matrix} 1, 5 = 2 a + b \\ - 3 = 8 a + b \end{matrix} \Leftrightarrow \{\begin{matrix} a = - \frac{3}{4} \\ b = 3 \end{matrix} .$

Vậy hàm số cần xác định là $y = - \frac{3}{4} x + 3.$

Xác định hàm số y=ax +b biết đồ thị (d) của nó đi qua A(1; 2,5) và B( 8, -3) Khi đó hãy tính: (ảnh 1)

Câu 17:

b) Khoảng cách h từ gốc toạ độ O đến đường thẳng (d)

Xem đáp án

b) Vẽ đồ thị hàm số

Lập bảng

x	0	4
$y = - \frac{3}{4} x + 3.$	3	0

Đồ thị hàm số (d) là đường thẳng đi qua điểm $P (0; 3)$ và $Q (4; 0)$

Xét $Δ P O Q$ vuông tại O có: $\tan Q_{1} = \frac{O P}{O Q} = \frac{3}{4} \approx \tan 36^{o} 52^{'}$

Suy ra $\hat{Q_{1}} \approx 36^{o} 52^{'} .$

Do đó $α \approx 180 - 36^{o} 52^{'} = 143^{o} 8^{'} .$

Vẽ $O H ⊥ P Q .$ Tam giác OPQ vuông tại O, có $O H ⊥ P Q .$ nên:

$\frac{1}{O H^{2}} = \frac{1}{O P^{2}} + \frac{1}{O Q^{2}}$ hay $\frac{1}{h^{2}} = \frac{1}{3^{2}} + \frac{1}{4^{2}} = \frac{25}{144} .$ Do đó $h = \sqrt{\frac{144}{25}} = 2, 4.$

Câu 18:

Viết phương trình đường thẳng (d) có hệ số góc bằng 7 và đi qua điểm $M (2; 1) .$

Xem đáp án

Gọi phương trình đường thẳng là $y = a x + b$

Do đường thẳng (d) có hệ số góc bằng 7 và đi qua điểm ta có $\{\begin{cases} a = 7 \\ 1 = 7.2 + b \end{cases} \Leftrightarrow \{\begin{cases} a = 7 \\ b = - 13 \end{cases}$ .

Vậy $y = 7 x - 13$ .

Câu 19:

Vẽ đồ thị hàm số $y = 3 x + 2$ (1)

Xem đáp án

a) Vẽ đồ thị hàm số $y = 3 x + 2$

Lập bảng

x	0
$y = 3 x + 2$	2	0

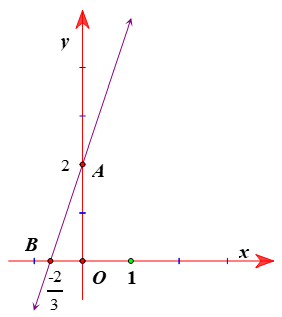
Đồ thị hàm số là đường thẳng đi qua $A (0, 2)$ và $B (\frac{- 2}{3}, 0)$

Câu 20:

b) Gọi A , B là giao điểm của đồ thị hàm số (1) với trục tung và trục hoành. Tính diện tích tam giác OAB .

Xem đáp án

b) Ta có OA = 2 và $O B = |\frac{- 2}{3}| = \frac{2}{3}$ . Tam giác OAB vuông tại O

$S_{O A B} = \frac{1}{2} O A . O B = \frac{1}{2} |2. \frac{- 2}{3}| = \frac{2}{3}$

.