Bài tập theo tuần Toán 9 - Tuần 26
-
1358 lượt thi
-
32 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 21:
Giải phương trình sau, bằng cách biến đổi chúng thành những phương trình mà vế trái là một bình phương còn vế phải là một hằng số :
 Xem đáp án
Xem đáp án
Câu 25:
Cho phương trình ẩn
Xác định m để phương trình có một nghiệm bằng 1.
 Xem đáp án
Xem đáp án
Phương trình có nghiệm bằng 1
Vậy thì thỏa đề
Câu 31:
Cho đường tròn (O; R), S là điểm sao cho OS = 2R, vẽ cát tuyến SCD đến đường tròn (O). C, D thuộc đường tròn (O). Cho biết . Tính SC và SD theo R
 Xem đáp án
Xem đáp án
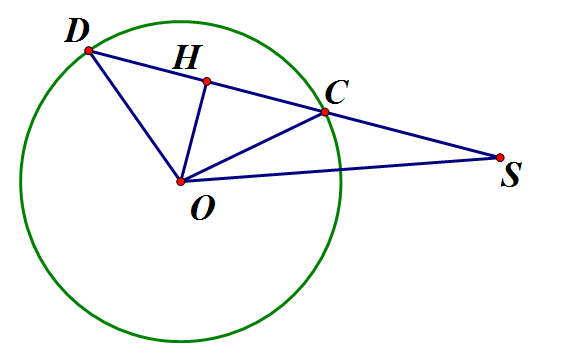
Ta có : là cạnh của tam giác đều nội tiếp Do đó
là tam giác nửa đều
có
. Do đó :
Câu 32:
Cho đường tròn tâm O bán kính R và hai dây AB, CD bất kỳ. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I, J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ // AB
 Xem đáp án
Xem đáp án
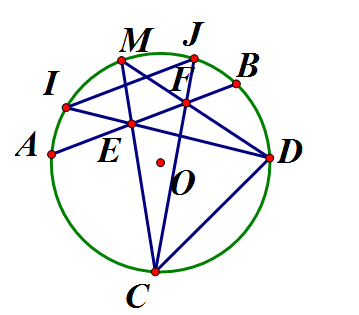
Ta có : (cùng bằng nửa số đo cung CM nhỏ )
là tứ giác nội tiếp
Từ đó (cùng chắn cung CE)
Lại có : (cùng chắn cung CI)
Vậy
