6 câu hỏi trắc nghiệm thuộc Dạng 1: Chứng minh qua 3 điểm xác định một góc bẹt (tổng hai góc chung đỉnh bằng 180 độ) có đáp án

Bài tập Toán 9 Chủ đề 5: Bài toán chứng minh ba điểm thẳng hàng có đáp án

Dạng 1: Chứng minh qua 3 điểm xác định một góc bẹt (tổng hai góc chung đỉnh bằng 180 độ) có đáp án

1620 lượt thi
6 câu hỏi
50 phút

Danh sách câu hỏi

Câu 1:

Cho tam giác ABC có các góc B và C nhọn, đường cao AH . Dựng ra phía ngoài tam giác ABC các tam giác vuông cân ABD, ACE( $\hat{B A D} = \hat{C A E} = 90^{o}$ ). Gọi M là trung điểm của DE. Chứng minh rằng H, A, M thẳng hàng.

Xem đáp án

Dựng hình bình hành $A E F D$ .

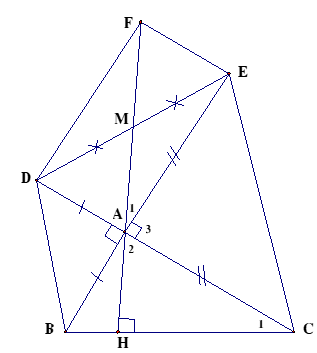
Cho tam giác ABC có các góc B và C nhọn, đường cao AH . Dựng ra phía ngoài tam giác ABC các tam giác vuông cân ABD, ACE (ảnh 1)

$\Rightarrow M$ là trung điểm của EF (t/c hình bình hành) và $E F = D A = B A$ .

Mặt khác $E A = C A$ (gt); $\hat{A E F} = \hat{C A B}$ (cùng bù với $\hat{D A E}$ ).

$\Rightarrow Δ E F A = Δ A B C$ (c – g – c).

$\hat{A_{1}} = \hat{C_{1}}$ ( Hai góc tương ứng).

Mà $\hat{A_{1}} + \hat{C_{1}} = 90^{o}$

$\Rightarrow \hat{A_{1}} + \hat{A_{2}} = 90^{o}$ .

$\Rightarrow \hat{A_{1}} + \hat{A_{2}} + \hat{A_{3}} = 180^{o}$ hay $\hat{F A H} = 180^{o} \Rightarrow M$ ,A , H thẳng hàng.

Câu 2:

Cho tam giác ABC vuông tại A. Đường tròn (O) đường kính AB cắt đường tròn (O’) đường kính AC tại D, M là điểm chính giữa cung nhỏ DC, AM cắt đường tròn (O) tại N, cắt BC tại E. Chứng minh O, N, O’thẳng hàng.

Xem đáp án

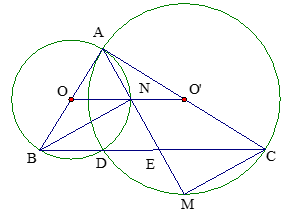
Cho tam giác ABC vuông tại A. Đường tròn (O) đường kính AB cắt đường tròn (O’) đường kính AC tại D, M là điểm chính giữa cung nhỏ (ảnh 1)

Xét (O’) có: $\hat{AEB} = \frac{sd \overset{⏜}{AD} + sd \overset{⏜}{CM}}{2}$ ( góc có đỉnh ở bên trong đường tròn).

$\hat{BAM} = \frac{sd \overset{⏜}{ADM}}{2} = \frac{sd \overset{⏜}{AD} + sd \overset{⏜}{MD}}{2}$ ( góc tạo bởi tia tiếp tuyến và dây cung) .

Suy ra $\hat{B A M} = \hat{AEB}$ Þ tam giác ABE cân tại B nên BN vừa là đường cao vừa là trung tuyến Þ NA = NE và OA = OB, O’A = O’C Þ NO, NO’ là đường trung bình của tam giác ACE, ABE nên O’N // CE, NO // EB do đó O, N, O’ thẳng hàng.

Câu 3:

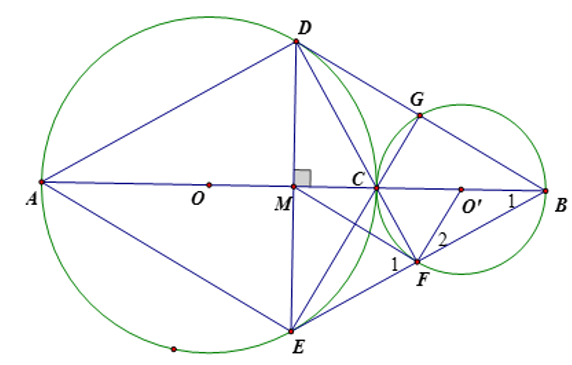
Hai đường tròn $(O; R)$ và $(O'; r)$ tiếp xúc ngoài tại $C (R > r)$ gọi AC và BC là hai đường kính đi qua C của đường tròn $(O)$ và $(O')$ . DE là dây cung của đường tròn $(O)$ vuông góc với AB tại trung điểm M của AB. Tia DC cắt đường tròn $(O')$ tại điểm thứ 2 là F

a) Tứ giác ADBE là hình gì? Vì sao?

Xem đáp án

Hai đường tròn (O,R) và (O',r) tiếp xúc ngoài tại C(R>r ) gọi AC và BC là hai đường kính đi qua C của đường tròn (ảnh 1)

a) Tứ giác ADBE là hình thoi vì AM = MB; MD = ME và

D E ⊥ A B

Câu 4:

b) Chứng minh ba điểm B, F, E thẳng hàng

Xem đáp án

b) Ta có

B E / / D A

. Nối BF ta có

\hat{A D F} = \hat{B F D} = 90^{0} \Rightarrow B F / / D A

. Như vậy

B E / / D A

và

B F / / D A

mà qua B chỉ có duy nhất một đường thẳng song song với DA do đó 3 điểm B, F, E phải thẳng hàng

Câu 5:

c) DB cắt đường tròn (O') tại điểm thứ hai là G. Chứng minh DF, EG và AB đồng quy

Xem đáp án

c) Ta có CG vuông góc với DB, mặt khác EC vuông góc với DB. Nhưng qua C chỉ tồn tại duy nhất một đường vuông góc với DB nên E, C , G phải thẳng hàng và DF, EG, AB phải đồng quy tại điểm C, chính là trực tâm tam giác EDB

Câu 6:

d) Chứng minh MF là tiếp tuyến của (O')

Xem đáp án

d) Nhận thấy $\hat{M E F} = \hat{F_{1}}$ và $\hat{O' B F} = \hat{F_{2}}$ mà $\hat{M E F} + \hat{O' B F} = 90^{0}$ nên $\hat{F_{1}} + \hat{F_{2}} = 90^{0}$ , suy ra $\hat{M F O'} = 90^{0}$ Vậy MF là tia tiếp tuyến của đường tròn tâm O’.

Bắt đầu thi ngay