8 câu hỏi trắc nghiệm thuộc Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 7)

Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 7)

Đề số 1

Ôn thi Cấp tốc 789+ vào 10 môn Toán (Đề 7)

103 lượt thi
8 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Trong mặt phẳng tọa độ Oxy cho Parabol (P): y = x² và đường thẳng (d): y = x + 2

a) Vẽ (P) và (d) trên cùng một hệ trục tọa độ.

b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 2:

Cho phương trình: 2x² - x - 3 = 0 có 2 nghiệm là x₁ , x₂ . Không giải phương trình, hãy tính giá trị của biểu thức $A = x_{1}^{2} + x_{2}^{2} - x_{1}^{2} x_{2}^{2} - 2024$ .

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 3:

Hợp tác xã A chuyên trồng hoa màu để bán. Nhưng năm nay chịu đợt sâu hại nên số lượng hoa màu dự định bán ra đã hư 30% và phần còn lại cũng ảnh hưởng nên chỉ bán được với giá bán bằng $\frac{3}{4}$ giá bán dự định lúc đầu. Nếu bán hết phần còn lại này với giá như trên thì số tiền sẽ ít hơn 152 triệu đồng so với dự tính lúc đầu. Hỏi nếu không bị hư hại và không giảm giá thì theo dự tính, hợp tác xã này sẽ thu về bao nhiêu tiền từ hoa màu?

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 4:

Một vé xem phim có mức giá là 60 000 đồng. Trong dịp khuyến mãi cuối năm 2019, số lượng người xem phim tăng thêm 45% nên tổng doanh thu cũng tăng 8,75%. Hỏi rạp phim đã giảm giá mỗi vé bao nhiêu phần trăm so với giá ban đầu?

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 5:

Có 2 đội công nhân cùng làm 1 công trình. Lần thứ nhất: đội 1 làm trong 6 ngày, đội 2 làm trong 4 ngày thì xong công trình. Lần thứ hai: đội 1 làm trong 4 ngày, đội 2 làm trong 8 ngày thì xong công trình. Hỏi nếu làm một mình thì mỗi đội công nhân làm trong bao lâu hoàn thành công trình?

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 6:

Một chiếc bàn hình tròn được ghép bởi hai nửa hình tròn đường kính 1,2m. Người ta muốn nới rộng mặt bàn bằng cách ghép thêm vào giữa một mặt hình chữ nhật có 1 kích thước là 1,2m như hình vẽ dưới.

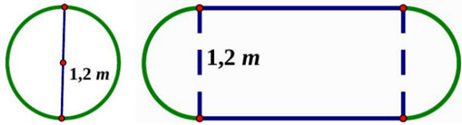
Một chiếc bàn hình tròn được ghép bởi hai nửa hình tròn đường kính 1,2m. Người ta muốn nới rộng mặt bàn bằng cách ghép thêm vào giữa một (ảnh 1)

a) Kích thước kia của hình chữ nhật phải là bao nhiêu để diện tích mặt bàn tăng gấp ba sau khi nới?

b) Kích thước kia của hình chữ nhật phải là bao nhiêu để chu vi mặt bàn tăng gấp đôi sau khi nới?

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 7:

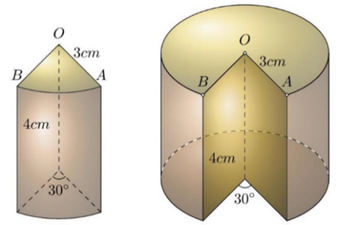
Một khối gỗ hình trụ có bán kính đáy là 3cm, chiều cao 4cm được đặt đứng trên mặt bàn. Một phần của khối gỗ bị cắt rời theo các bán kính OA, OB và theo chiều dài thẳng đứng từ trên xuống dưới với $\hat{A O B} = 30 °$ như hình vẽ bên.

a) Tính thể tích của khối gỗ còn lại sau khi bị cắt rời.

b) Diện tích toàn phần của khối gỗ còn lại sau khi đã bị cắt.

Một khối gỗ hình trụ có bán kính đáy là 3cm, chiều cao 4cm được đặt đứng trên mặt bàn. Một phần của khối gỗ bị cắt rời theo các bán kính OA, OB và theo chiều dài thẳng (ảnh 1)

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Câu 8:

Cho $Δ A B C$ nội tiếp trong đường tròn (O;R). Ba đường cao AD, BE, CF cắt nhau tại H

a) Chứng minh các tứ giác AEHF, BCEF nội tiếp.

b) Kẻ đường kính AK của (O). Chứng minh AB.AC = 2R.AD.

c) Gọi M là trung điểm của BC, I là giao điểm EF và BC. Chứng minh tứ giác EFDM nội tiếp và IB.IC = ID.IM.

Xem đáp án

Đề thi thử dành cho học sinh tự rèn luyện nên không có lời giải

Bắt đầu thi ngay