8 câu hỏi trắc nghiệm thuộc Dạng 1. Hệ thức về cạnh và đường cao trong tam giác vuông

Câu 1:

Cho tam giác ABC vuông tại A, BC = 20cm. Biết tỉ số hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là 9 : 16. Tính diện tích tam giác ABC.

Xem đáp án

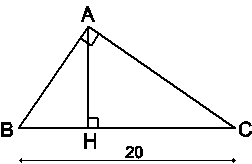
Vẽ đường cao AH.

Ta có $\frac{HB}{HC} = \frac{9}{16} \Rightarrow \frac{HB}{9} = \frac{HC}{16} = \frac{HB + HC}{9 + 16} = \frac{20}{25}$

Suy ra $HB = \frac{9.20}{25} = 7, 2$ (cm); $HC = \frac{16.20}{25} = 12, 8$ (cm)

Xét DABC vuông tại A, đường cao AH ta có:

$A B^{2} = B C . B H = 20.7, 2 = 144$ Þ AB = 12 (cm);

$A C^{2} = B C . C H = 20.12, 8 = 256$ Þ AC = 16 (cm).

Vậy diện tích DABC là $S = \frac{1}{2} ABAC = \frac{1}{2} \cdot 12.16 = 96$ (cm²).

Cách giải khác:

Sau khi tính được HB và HC, ta tính AH theo công thức: $A H^{2} = H B . H C$ (hệ thức 2).

$A H^{2} = 7, 2.12, 8 = 92, 16$ Þ AH = 9,6 (cm).

Diện tích DABC là $S = \frac{1}{2} BCAH = \frac{1}{2} \cdot 20.9, 6 = 96$ (cm²).

Câu 2:

Cho tam giác vuông với các cạnh góc vuông có độ dài là 3 cm và 4 cm , kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và các đoạn thẳng mà nó chia ra trên cạnh huyền.

Xem đáp án

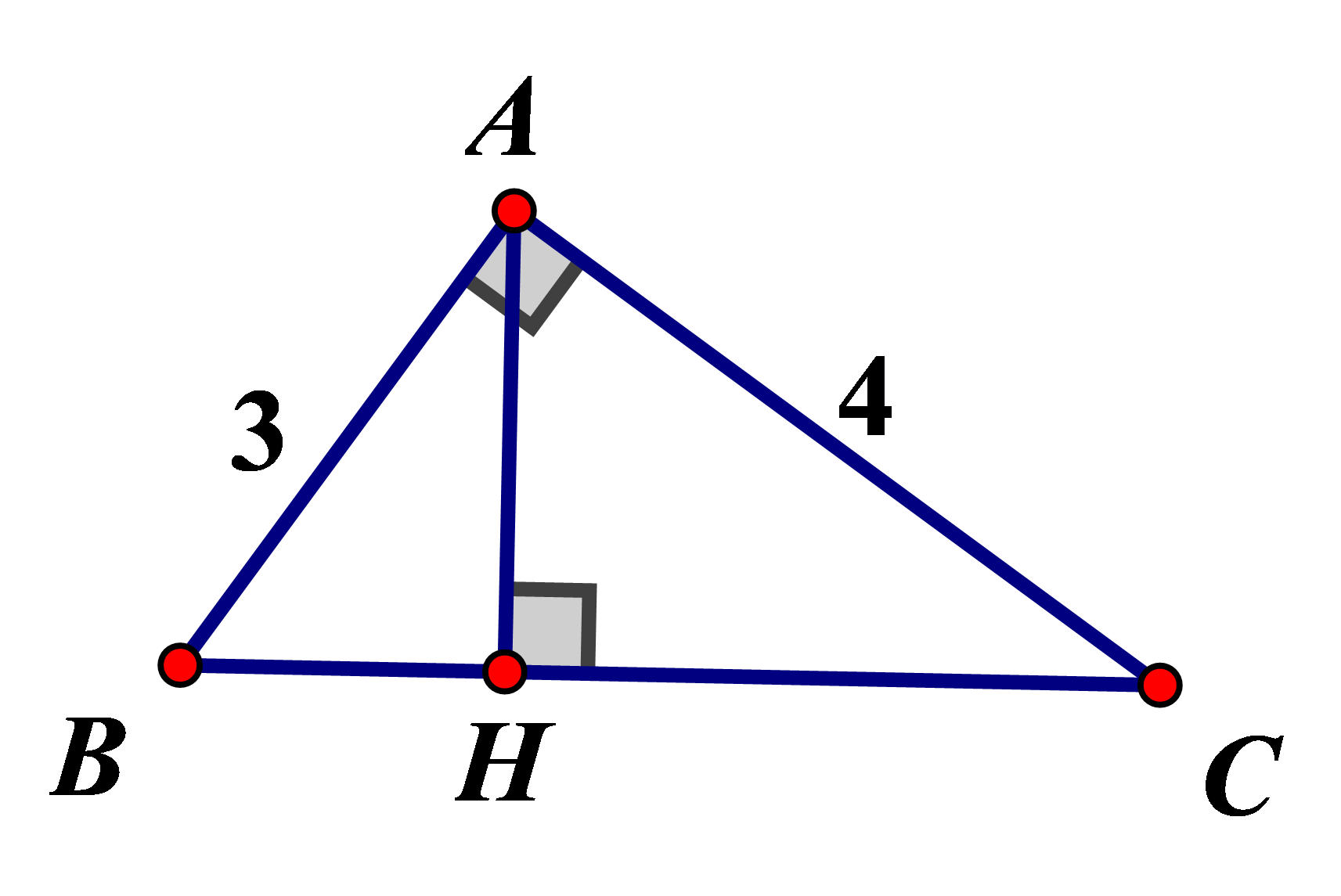
Media VietJack

Giả sử tam giác ABC có các cạnh góc vuông AB = 3cm, AC = 4cm, AH là đường cao.

Áp dụng định lí Pitago cho tam giác vuông ABC:

$B C^{2} = A B^{2} + A C^{2} = 3^{2} + 4^{2} = 25 \Rightarrow B C = 5$ cm

Áp dụng hệ thức lượng trong tam giác vuông ta có:

$B A^{2} = B H . B C \Rightarrow B H = \frac{B A^{2}}{B C} \Rightarrow B H = \frac{3^{2}}{5} \Rightarrow B H = \frac{9}{5}$ (cm)

$C A^{2} = C H . C B \Rightarrow C H = \frac{C A^{2}}{C B} \Rightarrow C H = \frac{4^{2}}{5} \Rightarrow C H = \frac{16}{5}$ (cm)

$A H^{2} = H B . H C \Rightarrow A H^{2} = \frac{9}{5} . \frac{16}{5} \Rightarrow A H = \frac{12}{5}$ (cm)

(Có thể tính đường cao AH bởi công thức $\frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}}$ )

Câu 3:

Cho tam giác ABC cân tại A. Các tia phân giác của góc A và góc B cắt nhau tại O. Biết $OA = 2 \sqrt{3}$ cm, OB = 2cm, tính độ dài AB.

Xem đáp án

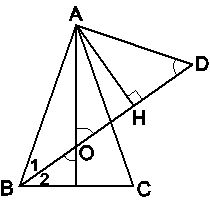
Qua A vẽ một đường thẳng vuông góc với AB cắt tia BO tại D.

Ta có $\hat{D} + \hat{B_{1}} = 90^{°}$

mà $\hat{B_{1}} = \hat{B_{2}}$ nên $\hat{A O D} = \hat{D}$

Do đó DAOD cân tại A. Suy ra $A D = A O = 2 \sqrt{3}$ (cm).

Vẽ AH ^ OD thì HO = HD.

Ta đặt $H O = H D = x$ thì $B D = 2 x + 2.$

Xét DABD vuông tại A, đường cao AH, ta có $A D^{2} = B D . H D .$

Suy ra ${(2 \sqrt{3})}^{2} = x (2 x + 2)$ Từ đó ta được phương trình:

$2 x^{2} + 2 x - 12 = 0$ Û (x – 2)(x + 3) = 0 Û x = 2 hoặc x = -3.

Giá trị x = 2 được chọn, giá trị x = -3 bị loại.

Do đó $B D = 2 + 2 + 2 = 6$ (cm). Suy ra $A B = \sqrt{6^{2} - {(2 \sqrt{3})}^{2}} = \sqrt{24} = 2 \sqrt{6}$ (cm).

Câu 4:

Cho tam giác ABC vuông tại A, đường cao AH. Biết diện tích các tam giác ABH và ACH lần lượt là 54cm² và 96cm². Tính độ dài BC.

Xem đáp án

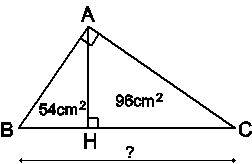
Media VietJack

Ta có $S_{A B H} = \frac{1}{2} A H B H = 54$

Suy ra $A H . B H = 108$ . (1)

$S_{ACH} = \frac{1}{2} AH . CH = 96$ Suy ra $A H . C H = 192$ . (2)

Từ (1) và (2) ta được: $A H^{2} . B H . C H = 108.192.$

Mặt khác $A H^{2} = B H . C H$ (hệ thức 2). Suy ra $A H^{4} = 12^{4}$ Þ AH = 12 (cm).

Ta có $S_{A B C} = 54 + 96 = 150$ (cm²) mà $S_{A B C} = \frac{1}{2} B C A H$ nên $\frac{1}{2} BCAH = 150$

Suy ra $BC = \frac{150.2}{12} = 25$ (cm).

Câu 5:

Cho hình thang ABCD,

\hat{A} = \hat{D} = 90^{0}

. Hai đường chéo vuông góc với nhau tại O. Biết OB = 5,4cm; OD = 15cm.

Qua O vẽ một đường thẳng song song với hai đáy, cắt AD và BC lần lượt tại M và N. Tính độ dài MN.

Xem đáp án

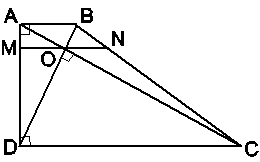
Media VietJack

Xét DADC có OM // CD nên $\frac{OM}{CD} = \frac{AO}{AC}$ (hệ quả của định lí Ta lét). (1)

Xét DBDC có ON // CD nên $\frac{ON}{CD} = \frac{BN}{BC}$ (hệ quả của định lí Ta-lét). (2)

Xét DABC có ON // AB nên $\frac{A O}{A C} = \frac{B N}{B C}$ (định lí Ta-lét). (3)

Từ (1), (2), (3) suy ra $\frac{OM}{CD} = \frac{ON}{CD}$

Do đó OM = ON.

Xét DAOD vuông tại O, OM ^ AD nên $\frac{1}{{OM}^{2}} = \frac{1}{{OA}^{2}} + \frac{1}{{OD}^{2}}$ (hệ thức 4).

Do đó $\frac{1}{{OM}^{2}} = \frac{1}{9^{2}} + \frac{1}{15^{2}} \Rightarrow OM \approx 7, 7$ (cm).

Suy ra $M N \approx 7, 7.2 = 15, 4$ (cm).

Câu 6:

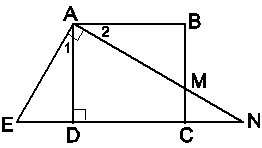
Cho hình vuông ABCD cạnh 1. Gọi M là một điểm nằm giữa B và C. Tia AM cắt đường thẳng CD tại N. Tính giá trị của biểu thức $P = \frac{1}{{AM}^{2}} + \frac{1}{{AN}^{2}}$

Xem đáp án

Tìm cách giải

Biểu thức $\frac{1}{{AM}^{2}} + \frac{1}{{AN}^{2}}$ gợi ý cho ta vận dụng hệ thức (4) $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$ để giải. Muốn vậy phải tạo ra một tam giác vuông có các cạnh góc vuông bằng AM, AN.

* Trình bày lời giải

Qua A vẽ một đường thẳng vuông góc với AM cắt đường thẳng CD tại E.

DADE và DABM có $\hat{D} = \hat{B} = 90^{°};$ AD = AB; $\hat{A_{1}} = \hat{A_{2}}$ (cùng phụ với $\hat{D A M}$ ).

Do đó $Δ A D E = Δ A B M (g . c . g) .$ Suy ra AE = AM.

Xét DAEN vuông tại A có AD ^ EN nên $\frac{1}{{AE}^{2}} + \frac{1}{{AN}^{2}} = \frac{1}{{AD}^{2}}$

Mặt khác $A E = A M; A D = 1$ nên $\frac{1}{{AM}^{2}} + \frac{1}{{AN}^{2}} = 1$

Câu 7:

Cho tam giác ABC cân tại A có các đường cao AH và BK. Chứng minh rằng : $\frac{1}{B K^{2}} = \frac{1}{B C^{2}} + \frac{1}{4 A H^{2}}$

Xem đáp án

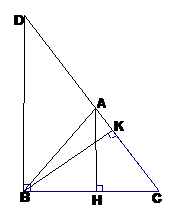
* Tìm cách giải: Để chứng minh đẳng thức trên người ta thường nghĩ ngay đến hệ thức lượng trong tam giác vuông “ Hệ thức $\frac{1}{h^{2}} = \frac{1}{b^{2}} + \frac{1}{c^{2}}$ ’’. Một thủ thuật để nhận ra tam giác vuông có đường cao ứng với cạnh huyền là vẽ đường phụ để tạo ra tam giác vuông tại B có đường cao là BK, cạnh góc vuông là BC. Khi đó ta nghĩ ngay đường phụ cần vẽ cạnh góc vuông còn lại.

* Trình bày lời giải

Qua B kẻ đường thẳng vuông góc với BC cắt tia đối của tia AC tại D.

Vì ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến $\Rightarrow$ BH = HC.

Xét BCD có BH = HC (c/m trên) ; AH // BD ( $⊥$ BC )

$\Rightarrow$ CA = AD (t/c đường trung bình của tam giác ).

Nên AH là đường trung bình của $Δ$ BCD

AH = $A H = \frac{1}{2} B D \Rightarrow$ BD = 2AH. (1)

Xét BCD có $\hat{D B C} = 90^{0}$ ; BK $⊥$ CD ( K $\in$ CD )

$\Rightarrow \frac{1}{B K^{2}} = \frac{1}{B C^{2}} + \frac{1}{B D^{2}}$ (2)

Từ (1) và (2) $\Rightarrow \frac{1}{B K^{2}} = \frac{1}{B C^{2}} + \frac{1}{4 A H^{2}}$ (đpcm)

Câu 8:

Cho hình thang ABCD, $\hat{A} = \hat{D} = 90^{°} =$ hai đường chéo vuông góc với nhau tại O. Cho biết AD = 12cm; CD = 16cm. Tính các độ dài OA, OB, OC, OD.

Xem đáp án

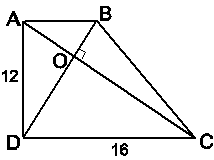
Media VietJack

DADC vuông tại D, theo định lí Py-ta-go ta có:

$A C^{2} = A D^{2} + D C^{2} = 12^{2} + 16^{2} = 400$ .

Suy ra AC = 20 (cm).

DADC vuông tại D, DO là đường cao nên $A D . D C = A C . D O$ (hệ thức 3).

Suy ra $OD = \frac{ADDC}{AC} = \frac{12.16}{20} = 9, 6$ (cm).

Ta lại có $A D^{2} = A C . A O$ (hệ thức 1) nên $OA = \frac{{AD}^{2}}{AC} = \frac{12^{2}}{20} = 7, 2$ (cm).

Do đó $O C = 20 - 7, 2 = 12, 8$ (cm).

Xét DABD vuông tại A, AO là đường cao nên $A O^{2} = O B . O D$ (hệ thức 2).

$\Rightarrow OB = \frac{{AO}^{2}}{OD} = \frac{7, 2^{2}}{9, 6} = 5, 4$ (cm).