5 câu hỏi trắc nghiệm thuộc Ôn thi Cấp tốc 789+ vào 10 môn Toán khu vực Bà Rịa - Vũng Tàu 2024 - 2025 (Đề 19)

Câu 1:

1) Giải phương trình: ${x^2} - 7x + 12 = 0$.

2) Giải hệ phương trình: $\left\{ {\begin{array}{*{20}{l}}{3x - y = 3}\\{x + 2y = 8}\end{array}} \right.$.

3) Rút gọn biểu thức: $A = \frac{3}{{2 - \sqrt 3 }} - \sqrt {75} + \frac{{2\sqrt {33} }}{{\sqrt {11} }}$.

1) ${x^2} - 7x + 12 = 0$. Ta có $\Delta = {\left( { - 7} \right)^2} - 4 \cdot 1 \cdot 12 = 1 > 0$.

Do đó, phương trình đã cho có hai nghiệm phân biệt $x = \frac{{7 + \sqrt 1 }}{2} = 4\,;\,\,x = \frac{{7 - \sqrt 1 }}{2} = 3$.

b) $\left\{ {\begin{array}{*{20}{l}}{3x - y = 3}\\{x + 2y = 8}\end{array}} \right.$. Nhân hai vế của phương trình thứ nhất với 2, ta được: $\left\{ {\begin{array}{*{20}{l}}{6x - 2y = 6}\\{x + 2y = 8}\end{array}} \right..$

Trừ từng vế hai phương trình của hệ mới, ta được $7x = 14$ hay $x = 2$.

Thế $x = 2$ vào phương trình thứ hai của hệ mới, ta có $2 + 2y = 8$ hay $2y = 6$, suy ra $y = 3.$

Vậy hệ phương trình đã cho có nghiệm là $\left( {2\,;\,3} \right).$

c) Ta có $A = \frac{3}{{2 - \sqrt 3 }} - \sqrt {75} + \frac{{2\sqrt {33} }}{{\sqrt {11} }}$

$ = \frac{{3\left( {2 + \sqrt 3 } \right)}}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}} - \sqrt {25 \cdot 3} + \frac{{2\sqrt 3 \cdot \sqrt {11} }}{{\sqrt {11} }}$

$ = 3\left( {2 + \sqrt 3 } \right) - 5\sqrt 3 + 2\sqrt 3 $

$ = 6 + 3\sqrt 3 - 5\sqrt 3 + 2\sqrt 3 = 6$.

Vậy $A = 6$.

Câu 2:

Cho parabol $\left( P \right):y = \frac{1}{2}{x^2}$ và đường thẳng $\left( a \right):y = - mx + 3$ (với $m$ là tham số).

1) Vẽ parabol $\left( P \right)$.

2) Tìm tất cả giá trị của tham số $m$ để $\left( d \right)$ thỏa mãn cắt $\left( P \right)$ tại hai điểm phân biệt có hoành độ \[{x_1},\,\,{x_2}\] thỏa mãn ${x_1}\left( {x_2^2 - 6} \right) = 24$.

Xem đáp án

1) Tập xác định $D = \mathbb{R}$. Bảng giá trị:

$x$	$ - 2$	$ - 1$	0	1	2
$y = \frac{1}{2}{x^2}$	2	$\frac{1}{2}$	0	$\frac{1}{2}$	2

Đồ thị hàm số $y = \frac{1}{2}{x^2}$ là parabol nhận \[Oy\] làm trục đối xứng, có đỉnh $O\left( {0\,;\,\,0} \right),$ bề lõm hướng lên và đi qua các điểm \[\left( { - 1\,;\,\,\frac{1}{2}} \right),\,\,\left( {1\,;\,\,\frac{1}{2}} \right),\,\]$\left( { - 2\,;\,\,2} \right),\,\,\left( {2\,;\,\,2} \right).$

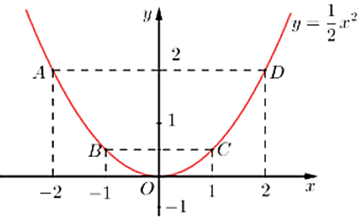
Đồ thị hàm số là đường cong parabol đi qua các điểm $O\left( {0\,;\,\,0} \right);\,\,A\left( { - 2\,;\,\,2} \right);\,\,B\left( { - 1;\,\,\frac{1}{2}} \right);$$C\left( {1;\,\,\frac{1}{2}} \right);\,\,D\left( {2;\,\,2} \right).$

Hệ số $a = \frac{1}{2} > 0$ nên parabol có bề cong hướng lên, đồ thị hàm số nhận \[Oy\] làm trục đối xứng.

Ta vẽ được đồ thị hàm số $y = \frac{1}{2}{x^2}$ như sau:

Cho parabol P:y = 1/2x^2 và đường thẳng a:y = - mx + 3 (với m là tham số). 1) Vẽ parabol P (ảnh 1)

2) Xét phương trình hoành độ giao điểm của $\left( d \right)$ và $\left( P \right)$, ta có:

$\frac{1}{2}{x^2} = - mx + 3$ hay $\frac{1}{2}{x^2} + mx - 3 = 0.$

Xét $\Delta = {m^2} - 4 \cdot \frac{1}{2} \cdot \left( { - 3} \right) = {m^2} + 6 > 0$ nên phương trình có hai nghiệm phân biệt.

Áp dụng định lí Viète, ta có: $\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - m}}{{\frac{1}{2}}} = - 2m}\\{{x_1} \cdot {x_2} = \frac{{ - 3}}{{\frac{1}{2}}} = - 6}\end{array}} \right.$.

Khi đó ${x_1}\left( {x_2^2 - 6} \right) = 24$ hay ${x_1}\left( {x_2^2 + {x_1}{x_2}} \right) = 24$ nên ${x_1}{x_2}\left( {{x_2} + {x_1}} \right) = 24$

Suy ra $ - 6 \cdot \left( { - 2m} \right) = 24$, suy ra $12m = 24$ hay $m = 2$.

Vậy $m = 2$ thỏa mãn yêu cầu bài toán.

Câu 3:

1) Nhân dịp Quốc tế thiếu nhi, trường trung học cơ sở $A$ tổ chức đi thăm và trao quà cho các em tại một mái ấm tình thương. Ban tổ chức giao cho một nhóm học sinh chuyến 120 phần quà lên khu vực trao quà. Tuy nhiên, khi thực hiện thì có 2 học sinh được phân công làm việc khác, nên mỗi học sinh còn lại trong nhóm phải chuyển nhiều hơn so với đự kiến 2 phần quà. Tính số học sinh trong nhóm dự kiến lúc đầu.

2) Giải phương trình: $\sqrt {x + 4} + \sqrt {1 - 2x} = 3$.

Xem đáp án

1) Gọi số học sinh dự kiến là $x$ (học sinh). Điều kiện $x \in \mathbb{N}*,\,\,x > 2.$

Dự kiến mỗi học sinh chuyển số phần quà là: $\frac{{120}}{x}$ (phần quà).

Thực tế số học sinh là: $x - 2$ (học sinh).

Thực tế mỗi học sinh chuyển số phần quà là: $\frac{{120}}{{x - 2}}$ (phần quà).

Vì thực tế mỗi học sinh phải chuyển nhiều hơn so với dự kiến 2 phần quà nên ta có phương trình $\frac{{120}}{x} + 2 = \frac{{120}}{{x - 2}}$

\[120\left( {x - 2} \right) + 2x\left( {x - 2} \right) = 120x\]

\[120x - 240 + 2{x^2} - 4x = 120x\]

\[{x^2} - 2x - 120 = 0\]

$x = 12$ (thỏa mãn điều kiện) hoặc $x = - 10$ (không thỏa mãn điều kiện).

Vậy dự kiến có 12 học sinh.

2) Ta có $\sqrt {x + 4} + \sqrt {1 - 2x} = 3$ (điều kiện $ - 4 \le x \le \frac{1}{2}\,).$

$x + 4 + 1 - 2x + 2\sqrt {\left( {x + 4} \right)\left( {1 - 2x} \right)} = 9$

$2\sqrt {\left( {x + 4} \right)\left( {1 - 2x} \right)} - \left( {x + 4} \right) = 0$

$\sqrt {x + 4} \left( {2\sqrt {1 - 2x} - \sqrt {x + 4} } \right) = 0$

$\sqrt {x + 4} = 0$ hoặc $2\sqrt {1 - 2x} = \sqrt {x + 4} $

$x + 4 = 0$ hoặc $4\left( {1 - 2x} \right) = x + 4$

$x = - 4$ hoặc $4 - 8x = x + 4$

$x = - 4$ (thỏa mãn) hoặc $x = 0$ (thỏa mãn).

Vậy phương trình đã cho có nghiệm $x = - 4$ và $x = 0$.

Câu 4:

Từ điểm $P$ nằm ngoài đường tròn $\left( O \right),$ kẻ hai tiếp tuyến \[PA,{\rm{ }}PB\] của đường tròn $(A,\,\,B$ là hai tiếp điểm). Gọi $H$ là giao điểm của \[PO\] và \[AB.\]

1) Chứng minh tứ giác \[PAOB\] nội tiếp.

2) Chứng minh $P{A^2} = PH \cdot PO.$

3) Điểm $N$ trên cung lớn \[AB\] của đường tròn $\left( O \right)$ sao cho tam giác \[NAB\] nhọn và $NA > NB.$ Đường thẳng \[PN\] cắt $\left( O \right)$ tại điểm $M$ khác $N.$ Chứng minh $\widehat {OMN} = \widehat {OHN}$.

4) Đường thẳng qua $N$ song song với \[PO\] cá́t đường thẳng \[AO\] tại $K$. Gọi $I$ là trung điểm của \[MN.\] Chúng minh đường thẳng \[KI\] vuông góc với đường thẳng \[AM.\]

Xem đáp án

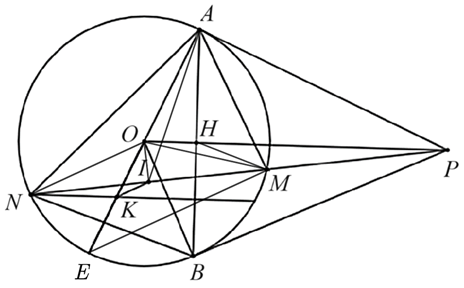
$Từ điểm P nằm ngoài đường tròn O kẻ hai tiếp tuyến PA, PB của đường tròn \A, B là hai tiếp điểm). Gọi H là giao điểm của (ảnh 1)$

1) Do \[PA,{\rm{ }}PB\] là tiếp tuyến nên $\widehat {OAP} = \widehat {OBP} = 90^\circ .$

Xét tứ giác \[PAOB\] có

$\widehat {OAP} + \widehat {OBP} = 90^\circ + 90^\circ = 180^\circ $.

Mà $\widehat {OAP},\,\,\widehat {OBP}$ ở vị trí đối diện nên tứ giác \[PAOB\] nội tiếp.

2) Ta có $PA = PB$ (tính chất hai tiếp tuyến cắt nhau), $OA = OB = R$ nên $PO$ là trung trực của \[AB.\]

Suy ra $PO \bot AB$ tại $H$ là trung điểm của \[AB.\]

Xét $\Delta PAH$ và $\Delta PAH$$\Delta POA$ có \[\widehat {PHA} = \widehat {PAO} = 90^\circ ;\] $\widehat {APH}$ chung.

Do đó .

Suy ra \[\frac{{PA}}{{PH}} = \frac{{PO}}{{PA}}\] hay $P{A^2} = PH \cdot PO$ (đpcm).

3) Xét $\Delta PBM$ và $\Delta PNB$ có $\widehat {BPM}$ chung và

Do đó suy ra \[\frac{{PB}}{{PN}} = \frac{{PM}}{{PB}}\] hay \[P{B^2} = PM \cdot PN = P{A^2}\].

Mà $P{A^2} = PH \cdot PO$ nên $PM \cdot PN = PH \cdot PO$ hay$\frac{{PM}}{{PO}} = \frac{{PH}}{{PN}}$.

Xét $\Delta PMH$ và $\Delta PON$ có $\widehat {OPN}$ chung; $\frac{{PM}}{{PO}} = \frac{{PH}}{{PN}}$ (cmt).

Do đó , suy ra $\widehat {PMH} = \widehat {PON}$ (hai góc tương ứng).

Mặt khác $\widehat {PMH} + \widehat {NMH} = 180^\circ $ (kề bù) nên $\widehat {PON} + \widehat {NMH} = 180^\circ $.

Mà $\widehat {PON},\,\,\widehat {NMH}$ nằm ở vị trí đối diện nên tứ giác $HMNO$ nội tiếp.

Suy ra $\widehat {OMN} = \widehat {OHN}$ (cùng chắn cung \[ON\,)\].

4) Kẻ đường kính \[AE\] của $\left( O \right)$. Do \[I\] là trung điểm của \[MN\] nên $OI \bot MN.$

Xét tam giác $OMN\,\,\left( {OM = ON} \right)$ có $OI$ là đường trung tuyến (vì \[I\] là trung điểm của \[MN)\]nên $OI$ cũng là đường cao hay $OI \bot MN.$

Suy ra \[\widehat {OIP} + \widehat {OAP} = 90^\circ + 90^\circ = 180^\circ \].

Mà \[\widehat {OIP},\,\,\widehat {OAP}\] nằm ở trị trí đối diện nên tứ giác $OIPA$ nội tiếp.

Suy ra \[\widehat {IPO} = \widehat {IAO}\] (cùng chắn cung \[IO\,)\]

Mà $\widehat {IPO} = \widehat {INK}$ (\[OP\,{\rm{//}}\,NK\], so le trong) nên $\widehat {IAO} = \widehat {INK}$.

Chứng minh bổ đề: Cho tứ giác $ABCD$ có $\widehat {ACB} = \widehat {ADB}.$ Chứng minh tứ giác $ABCD$ là tứ giác nội tiếp.

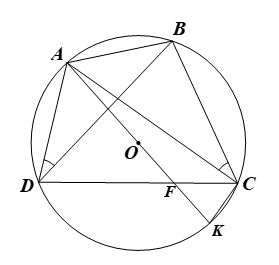
$Từ điểm P nằm ngoài đường tròn O kẻ hai tiếp tuyến PA, PB của đường tròn \A, B là hai tiếp điểm). Gọi H là giao điểm của (ảnh 2)$

• Giả sử $\Delta ABC$ có đường tròn ngoại tiếp tâm $O$ và đường kính $AK$ nên tứ giác $ABCK$ nội tiếp, suy ra $\widehat {ACB} = \widehat {AKB}$ (hai góc nội tiếp cùng chắn cung $AB).$

Mà $\widehat {ACB} = \widehat {ADB}$ (giả thiết) nên $\widehat {ADB} = \widehat {AKB}.$ $\left( 6 \right)$

⦁ Gọi $F$ là giao điểm của $AK$ và $BD,$ $F$ nằm trong đường tròn $\left( O \right).$

Xét $\Delta AFD$ và $\Delta BFK$ có: $\widehat {AFD} = \widehat {BFK}$ (đối đỉnh) và $\widehat {ADF} = \widehat {BKF}$ (chứng minh trên)

Do đó suy ra $\frac{{AF}}{{BF}} = \frac{{DF}}{{KF}}$ nên $\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}.$

Xét $\Delta DFK$ và $\Delta AFB$ có: $\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}$ và \[\widehat {DFK} = \widehat {AFB}\] (đối đỉnh)

Do đó suy ra $\widehat {FDK} = \widehat {FAB}.\,\,\,\left( 7 \right)$

⦁ Ta có $\widehat {ABK}$ là góc nội tiếp chắn nửa đường tròn nên $\widehat {ABK} = 90^\circ ,$ do đó $\Delta ABK$ vuông tại $B,$ suy ra $\widehat {FAB} + \widehat {AKB} = 90^\circ .\,\,\,\left( 8 \right)$

Từ $\left( 6 \right),\,\,\left( 7 \right),\,\,\left( 8 \right)$ suy ra $\widehat {ADB} + \widehat {FDK} = 90^\circ $ hay $\widehat {ADK} = 90^\circ .$

Khi đó $\Delta ADK$ vuông tại $D$ nên điểm $D$ nằm trên đường tròn đường kính $AK.$

Suy ra tứ giác $ABCD$ nội tiếp đường tròn $\left( O \right)$ đường kính $AK.$

Áp dụng bổ đề trên cho tứ giác $IKNA$ có $\widehat {IAO} = \widehat {INK}$ nên tứ giác $IKNA$ nội tiếp.

Suy ra \[\widehat {NIK} = \widehat {NAK}\] (cùng chắn cung \[NK\]).

Mà $\widehat {NAK} = \widehat {NME}$ (cùng chắn cung \[NE\]) nên \[\widehat {NIK} = \widehat {NME}\] suy ra \[IK\,{\rm{//}}\,ME\] (hai góc đồng vị bằng nhau)

Mặt khác $\widehat {AME} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn) nên $ME \bot AM.$

Do đó $NK \bot AM$ (đpcm).

Câu 5:

Tìm giá trị lớn nhất của biểu thức: $P = x\left( {\sqrt {12 - 3{x^2}} + 1 - {x^2}} \right)$, với $x$ là số thực thỏa mãn $0 \le x \le 2$.

Xem đáp án

Ta có $P = x\left( {\sqrt {12 - 3{x^2}} + 1 - {x^2}} \right) = x\sqrt {12 - 3{x^2}} + x - {x^3}$.

Áp dụng bất đẳng thức Cauchy, ta có:

$x\sqrt {12 - 3{x^2}} = \frac{{2 \cdot 3x\sqrt {12 - 3{x^2}} }}{6} \le \frac{{9{x^2} + 12 - 3{x^2}}}{6} = {x^2} + 2$.

Suy ra \[P \le {x^2} + 2 + x - {x^3} = - {\left( {x - 1} \right)^2}\left( {x + 1} \right) + 3 \le 3\].

Dấu xảy ra khi và chỉ khi $x = 1$.

\(x\)	\( - 2\)	\( - 1\)	0	1	2
\(y = \frac{1}{2}{x^2}\)	2	\(\frac{1}{2}\)	0	\(\frac{1}{2}\)	2