15 câu trắc nghiệm Toán 9 Kết nối tri thức Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên có đáp án
15 câu trắc nghiệm Toán 9 Kết nối tri thức Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên có đáp án
-
53 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Chu vi đường tròn có bán kính \[R = 9\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Chu vi đường tròn có bán kính \[R = 9\] là: \[C = 2\pi R = 2\pi \cdot 9 = 18\pi .\]
Vậy chu vi đường tròn có bán kính \[R = 9\] là \[18\pi .\]
Do đó ta chọn phương án B.
Câu 2:
Công thức tính diện tích hình vành khuyên tạo bởi hai đường tròn đồng tâm có bán kính \[R\] và \[r\] (với \[R > r)\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Công thức tính diện tích hình vành khuyên tạo bởi hai đường tròn đồng tâm có bán kính \[R\] và \[r\] (với \[R > r)\] là: \[{S_v} = \pi \left( {{R^2} - {r^2}} \right).\]
Vậy ta chọn phương án C.
Câu 3:
Tỉ số giữa độ dài cung \[n^\circ \] và chu vi đường tròn (cùng bán kính) luôn bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Tỉ số giữa độ dài cung \[n^\circ \] và chu vi đường tròn (cùng bán kính) luôn bằng \[\frac{n}{{360}}.\]
Nghĩa là, \[\frac{l}{C} = \frac{n}{{360}}.\]
Vậy ta chọn phương án D.
Câu 4:
Phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung tròn đó được gọi là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hình quạt tròn là phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung tròn đó.
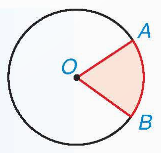
Vậy ta chọn phương án A.
Câu 5:
Độ dài cung \[30^\circ \] của một đường tròn có bán kính \[4{\rm{\;dm}}\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Độ dài cung tròn cần tìm là: \[l = \frac{n}{{180}}\pi R = \frac{{30}}{{180}}\pi \cdot 4 = \frac{{2\pi }}{3}{\rm{\;(dm)}}{\rm{.}}\]
Vậy độ dài cung tròn cần tìm bằng \[\frac{{2\pi }}{3}\,\,{\rm{dm}}.\]
Do đó ta chọn phương án B.
Câu 6:
II. Thông hiểu
Số đo \[n^\circ \] của cung tròn có độ dài \[30,8{\rm{\;cm}}\] trên đường tròn có bán kính \[22{\rm{\;cm}}\] (lấy \[\pi \approx 3,14\] và làm tròn đến độ) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có \[l = \frac{n}{{180}}\pi R.\]
Suy ra \[n = \frac{l}{{\pi R}} \cdot 180 \approx \frac{{30,8}}{{3,14 \cdot 22}} \cdot 180 \approx 80^\circ .\]
Vậy ta chọn phương án D.
Câu 7:
Cho tam giác \[ABC\] vuông tại \[A,\] cạnh \[AB = 5{\rm{\;cm}},\,\,\widehat {B\,} = 60^\circ .\] Đường tròn tâm \[I,\] đường kính \[AB\] cắt \[BC\] ở \[D.\] Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
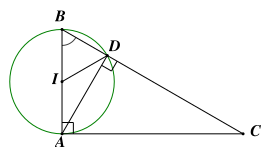
Vì \[IB = ID\] (cùng bằng bán kính của đường tròn \[\left( I \right)\] đường kính \[AB\]) nên tam giác \[IBD\] cân tại \[I.\]
Mà \[\widehat {IBD} = 60^\circ ,\] do đó tam giác \[IBD\] đều.
Suy ra \[\widehat {BID} = 60^\circ \] nên
Bán kính đường tròn \[\left( I \right)\] là: \[R = \frac{{AB}}{2} = \frac{5}{2}{\rm{\;(cm)}}{\rm{.}}\]
Độ dài cung nhỏ \[BD\] của đường tròn \[\left( I \right)\] là: \[l = \frac{n}{{180}}\pi R = \frac{{60}}{{180}}\pi \cdot \frac{5}{2} = \frac{{5\pi }}{6}{\rm{\;(cm)}}{\rm{.}}\]
Vì vậy phương án A sai, phương án D đúng.
Vậy ta chọn phương án A.
Câu 8:
Cho đường tròn \[\left( {O;10{\rm{\;cm}}} \right)\] đường kính \[AB.\] Điểm \[M \in \left( O \right)\] sao cho \[\widehat {BAM} = 45^\circ .\] Diện tích hình quạt \[AOM\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A

Vì \[OA = OM = 10{\rm{\;(cm)}}\] nên tam giác \[OAM\] cân tại \[O.\]
Mà \[\widehat {BAM} = 45^\circ \], suy ra tam giác \[OAM\] vuông cân tại \[O.\]
Do đó số đo cung nhỏ \[AM\] là:
Diện tích hình quạt \[AOM\] là: \[S = \frac{n}{{360}}\pi {R^2} = \frac{{90}}{{360}}\pi \cdot {10^2} = 25\pi {\rm{\;(c}}{{\rm{m}}^2}).\]
Vậy diện tích hình quạt \[AOM\] bằng \[25\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Do đó ta chọn phương án A.
Câu 9:
Cho đường tròn \[\left( O \right)\] đường kính \[AB = 2\sqrt 2 {\rm{\;cm}}.\] Điểm \[C \in \left( O \right)\] sao cho \[\widehat {ABC} = 30^\circ .\] Diện tích hình quạt \[BAC\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C

Ta có \[OB = OC\] nên tam giác \[OBC\] cân tại \[O.\] Suy ra \[\widehat {OCB} = \widehat {OBC} = 30^\circ .\]
Tam giác \[OBC\] có: \[\widehat {BOC} + \widehat {OCB} + \widehat {OBC} = 180^\circ \] (định lí tổng ba góc của một tam giác)
Suy ra \[\widehat {BOC} = 180^\circ - \left( {\widehat {OCB} + \widehat {OBC}} \right) = 180^\circ - \left( {30^\circ + 30^\circ } \right) = 120^\circ .\]
Do đó
Bán kính đường tròn \[\left( O \right)\] là: \[R = \frac{{AB}}{2} = \frac{{2\sqrt 2 }}{2} = \sqrt 2 {\rm{\;(cm)}}{\rm{.}}\]
Diện tích hình quạt \[BAC\] là: \[{S_q} = \frac{n}{{360}} \cdot \pi {R^2} = \frac{{240}}{{360}} \cdot \pi \cdot {\left( {\sqrt 2 } \right)^2} = \frac{{4\pi }}{3}{\rm{\;(c}}{{\rm{m}}^2}).\]
Vậy diện tích hình quạt \[BAC\] bằng \[\frac{{4\pi }}{3}{\rm{\;c}}{{\rm{m}}^2}.\]
Do đó ta chọn phương án C.
Câu 10:
Cho tam giác \[ABC\] đều có ba đỉnh nằm trên đường tròn \[\left( O \right).\] Độ dài các cung \[AB,BC,CA\] đều bằng \[6\pi {\rm{\;cm}}.\] Diện tích của đường tròn \[\left( O \right)\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D

Chu vi đường tròn \(\left( O \right)\) hay chính là độ dài đường tròn \[\left( O \right),\] và bằng \[6\pi + 6\pi + 6\pi = 18\pi .\]
Suy ra \[2\pi R = 18\pi \] hay \[R = 9{\rm{\;(cm)}}{\rm{.}}\]
Diện tích của đường tròn \[\left( O \right)\] là: \[S = \pi {R^2} = \pi \cdot {9^2} = 27\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Vậy ta chọn phương án D.
Câu 11:
Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có đường kính lần lượt là \[8{\rm{\;cm}}\] và \[6{\rm{\;cm}}\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Bán kính của hai đường tròn đồng tâm lần lượt là \[R = \frac{8}{2} = 4{\rm{\;(cm)}}\] và \[r = \frac{6}{2} = 3{\rm{\;(cm)}}{\rm{.}}\]
Diện tích hình vành khuyên cần tìm là: \[{S_v} = \pi \left( {{R^2} - {r^2}} \right) = \pi \left( {{4^2} - {3^2}} \right) = 7\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Do đó diện tích hình vành khuyên cần tìm là \[7\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Vậy ta chọn phương án B.
Câu 12:
Cho hình vành khuyên giới hạn bởi hai đường tròn \[\left( {O;R} \right)\] và \[\left( {O;r} \right),\] biết rằng \[r = 7{\rm{\;cm}}\] và \[R\] gấp \[3\] lần \[r\]. Diện tích của hình vành khuyên đó bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Bán kính \[R = 3r = 3 \cdot 7 = 21{\rm{\;(cm)}}{\rm{.}}\]
Diện tích của hình vành khuyên đó là: \[{S_v} = \pi \left( {{R^2} - {r^2}} \right) = \pi \left( {{{21}^2} - {7^2}} \right) = 392\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Do đó diện tích của hình vành khuyên đó bằng \[392\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Vậy ta chọn phương án A.
Câu 13:
III. Vận dụng
Cho sân cỏ như hình vẽ, biết rằng \[OB = 10{\rm{\;m}},\,\,\widehat {AOB} = 80^\circ .\]
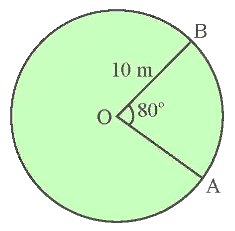
Độ dài đoạn hàng rào quanh sân từ \[A\] đến \[B\] của sân cỏ (làm tròn kết quả đến hàng phần trăm) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Độ dài đoạn hàng rào từ \[A\] đến \[B\] của sân cỏ là:
\[l = \frac{n}{{180}}\pi R = \frac{{80}}{{180}}\pi \cdot 10 = \frac{{40\pi }}{9} \approx 13,96{\rm{\;(m)}}{\rm{.}}\]
Do đó độ dài đoạn hàng rào từ \[A\] đến \[B\] của sân cỏ bằng khoảng \[13,96{\rm{\;m}}.\]
Vậy ta chọn phương án C.
Câu 14:
Cho hình “viên phân” (phần màu xanh) được giới hạn bởi dây cung có độ dài \[55{\rm{\;cm}}\] và cung có số đo \[95^\circ \] (hình vẽ).
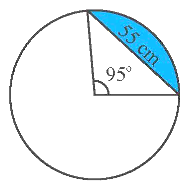
Diện tích hình viên phân đó (làm tròn kết quả đến hàng phần trăm) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
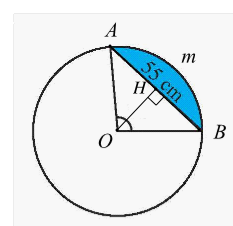
Kẻ \[OH \bot AB\] tại \[H.\]
Tam giác \[OAB\] cân tại \[O\] (do \[OA = OB = R\]) có \[OH\] là đường cao, suy ra \[OH\] cũng là đường trung tuyến của tam giác. Do đó \[H\] là trung điểm \[AB.\]
Vì vậy \[HB = \frac{{AB}}{2} = \frac{{55}}{2} = {\rm{27,5\;(cm)}}{\rm{.}}\]
Tam giác \[OAB\] cân tại \[O\] có \[OH\] là đường cao, suy ra \[OH\] cũng là đường phân giác của tam giác.
Do đó \[\widehat {BOH} = \frac{{\widehat {AOB}}}{2} = \frac{{95^\circ }}{2} = 47,5^\circ .\]
Vì tam giác \[OBH\] vuông tại \[H\] nên:
⦁ \[\sin \widehat {BOH} = \frac{{HB}}{{OB}},\] suy ra \[OB = \frac{{HB}}{{\sin \widehat {BOH}}} = \frac{{27,5}}{{\sin 47,5^\circ }}{\rm{\;(cm);}}\]
⦁ \[\tan \widehat {BOH} = \frac{{HB}}{{OH}},\] suy ra \[OH = \frac{{HB}}{{\tan \widehat {BOH}}} = \frac{{27,5}}{{\tan 47,5^\circ }}{\rm{\;(cm)}}{\rm{.}}\]
Diện tích tam giác \[OAB\] là:
\[{S_{\Delta OAB}} = \frac{1}{2} \cdot OH \cdot AB = \frac{1}{2} \cdot \frac{{27,5}}{{\tan 47,5^\circ }} \cdot 55 = \frac{{3025}}{{4 \cdot \tan 47,5^\circ }} \approx 692,98{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Diện tích hình quạt tròn \[AOB\] là:
\[{S_{hqAOB}} = \frac{n}{{360}} \cdot \pi {R^2} = \frac{{95}}{{360}} \cdot \pi \cdot O{B^2} = \frac{{19}}{{72}} \cdot \pi \cdot {\left( {\frac{{27,5}}{{\sin 47,5^\circ }}} \right)^2} \approx 1\,\,153,39{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Khi đó, diện tích hình viên phân cần tìm là:
\[S = {S_{hqAOB}} - {S_{\Delta OAB}} \approx 1\,\,153,39 - 692,98 = 460,41{\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Vậy ta chọn phương án B.
Câu 15:
Hình vẽ dưới đây mô tả mặt cắt của một chiếc đèn led có dạng hai hình vành khuyên màu trắng với bán kính các đường tròn lần lượt là \[15{\rm{\;cm}},\,\,18{\rm{\;cm}},\,\,21{\rm{\;cm}},\,\,24{\rm{\;cm}}.\]

Khi đó tổng diện tích hai hình vành khuyên đó bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Diện tích hình vành khuyên màu trắng tạo bởi hai đường tròn đồng tâm có bán kính bằng \[15{\rm{\;cm}},\,\,18{\rm{\;cm}}\] là:
\[{S_1} = \pi \left( {{{18}^2} - {{15}^2}} \right) = 99\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Diện tích hình vành khuyên màu trắng tạo bởi hai đường tròn đồng tâm có bán kính bằng \[21{\rm{\;cm}},\,\,24{\rm{\;cm}}\] là:
\[{S_2} = \pi \left( {{{24}^2} - {{21}^2}} \right) = 135\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Tổng diện tích hai hình vành khuyên đó là:
\[S = {S_1} + {S_2} = 99\pi + 135\pi = 234\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Do đó tổng diện tích hai hình vành khuyên đó bằng \[234\pi {\rm{\;c}}{{\rm{m}}^2}{\rm{.}}\]
Vậy ta chọn phương án A.
