Đáp án đúng là: D

Căn bậc hai của một số \(a\) không âm (hay \(a \ge 0)\) là \(\sqrt a \) và \( - \sqrt a \).

Đáp án đúng là: B

Ta có \(\sqrt {64} = \sqrt {{8^2}} = 8\).

Vậy giá trị của biểu thức \(\sqrt {64} \) là 8.

Đáp án đúng là: D

Ta có \({\left( { - 5} \right)^2} = 25\).

Do \({5^2} = 25\) nên 25 có hai căn bậc hai là 5 và –5.

Vậy căn bậc hai của \({\left( { - 5} \right)^2}\) là 5 và –5.

Đáp án đúng là: B

Ta thấy \(64 = {4^3}\) nên căn bậc 3 của 64 là 4.

Đáp án đúng là: C

Với mọi \(x,\) ta có: \({\left( {\sqrt[3]{x}} \right)^3} = x\).

Đáp án đúng là: B

Ta có \({\left( {\frac{1}{9}} \right)^2} = \frac{1}{{81}}\) và \({\left( { - \frac{1}{9}} \right)^2} = \frac{1}{{81}}\) nên hai số \(\frac{1}{9}\) và \( - \frac{1}{9}\) là căn bậc hai của \(\frac{1}{{81}}\).

Đáp án đúng là: C

Ta có \({\left( {\frac{1}{{{a^3}}}} \right)^2} = {\left[ {{{\left( {\frac{1}{a}} \right)}^3}} \right]^2} = {\left( {\frac{1}{a}} \right)^6} = \frac{1}{{{a^6}}}.\)

Như vậy, \(\frac{1}{{{a^3}}}\) là căn bậc hai của \(\frac{1}{{{a^6}}}\).

Đáp án đúng là: D

Ta có \({\left( {\frac{1}{{{a^3}}}} \right)^3} = {\left[ {{{\left( {\frac{1}{a}} \right)}^3}} \right]^3} = {\left( {\frac{1}{a}} \right)^9} = \frac{1}{{{a^9}}}.\)

Như vậy, \(\frac{1}{{{a^3}}}\) là căn bậc ba của \(\frac{1}{{{a^9}}}\).

Đáp án đúng là: A

Ta có \({\left( {\sqrt a } \right)^2} = a\) với \(a \ge 0.\)

Đáp án đúng là: C

Ta có:

⦁ \(\frac{5}{4} > \frac{4}{5}\) nên \(\sqrt {\frac{5}{4}} > \sqrt {\frac{4}{5}} \).

⦁ \(\frac{2}{5} < \frac{1}{2}\) nên \(\sqrt {\frac{2}{5}} < \sqrt {\frac{1}{2}} \), do đó \( - \sqrt {\frac{2}{5}} > - \sqrt {\frac{1}{2}} \).

⦁ \[0,49 > 0,48\] nên \(\sqrt {0,49} > \sqrt {0,47} \)

Mà \[0,{7^2} = 0,49\] nên \(\sqrt {0,49} = 0,7\), do đó \(0,7 > \sqrt {0,48} .\)

⦁ \(\frac{1}{9} < \frac{1}{8}\) nên \(\sqrt {\frac{1}{9}} < \sqrt {\frac{1}{8}} \)

Mà \({\left( {\frac{1}{3}} \right)^2} = \frac{1}{9}\) nên \(\sqrt {\frac{1}{9}} = \frac{1}{3},\) do đó \(\frac{1}{3} < \sqrt {\frac{1}{8}} ,\) suy ra \( - \frac{1}{3} > - \sqrt {\frac{1}{8}} .\)

Vậy phương án C là nhận định sai, ta chọn phương án C.

Đáp án đúng là: C

Ta có:

⦁ \( - 13,12 < - 11,35\) nên \(\sqrt[3]{{ - 13,12}} < \sqrt[3]{{ - 11,35}}.\)

⦁ \(0,02 < \frac{1}{6}\) nên \(\sqrt[3]{{0,02}} < \sqrt[3]{{\frac{1}{6}}},\) do đó \( - \sqrt[3]{{0,02}} > - \sqrt[3]{{\frac{1}{6}}}.\)

⦁ \(\frac{1}{{125}} > \frac{1}{{126}}\) nên \(\sqrt[3]{{\frac{1}{{125}}}} > \sqrt[3]{{\frac{1}{{126}}}}\)

Mà \({\left( {0,2} \right)^3} = {\left( {\frac{1}{5}} \right)^3} = \frac{1}{{125}}\) nên \(\sqrt[3]{{\frac{1}{{125}}}} = 0,2\), do đó \(0,2 > \sqrt[3]{{\frac{1}{{126}}}},\) suy ra \( - 0,2 < - \sqrt[3]{{\frac{1}{{126}}}}\).

⦁ \(64\frac{1}{2} > 64\) nên \(\sqrt[3]{{64\frac{1}{2}}} > \sqrt[3]{{64}}\)

Mà \({4^3} = 64\) nên \(\sqrt[3]{{64}} = 4,\) do đó \(\sqrt[3]{{64\frac{1}{2}}} > 4\).

Vậy phương án C là nhận định sai, ta chọn phương án C.

Đáp án đúng là: B

Bấm máy tính theo thứ tự dưới đây:

$\boxed{\text{ 2 }}\boxed{\text{ + }}\boxed{\frac{■}{}}\boxed{\sqrt{}}\boxed{\text{ 3 }}\boxed{\nabla }\boxed{\text{ 2 }}\boxed{⊳}\boxed{\text{ + }}\boxed{\frac{■}{}}\boxed{\text{SHIFT}}\boxed{\sqrt{}}\boxed{\text{ 4 }}\boxed{\nabla }\boxed{\text{ 3 }}\boxed{\text{ = }}$

Ta được kết quả như sau:

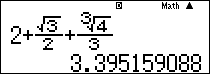
Làm tròn kết quả trên đến hàng phần trăm, ta được

\[2 + \frac{{\sqrt 3 }}{2} + \frac{{\sqrt[3]{4}}}{3} \approx 3,40.\]

Đáp án đúng là: B

Với \(x\) là số không âm, từ \(\sqrt x < 7\) ta có \({\left( {\sqrt x } \right)^2} < {7^2}\) hay \(x < {7^2}\) nên \(x < 49.\)

Mà \(x\) là số nguyên không âm nên ta có \(x \in \left\{ {0;\,\,1;\,\,2;\,\,...;\,\,48} \right\}.\)

Như vậy, \(S = \left\{ {0;\,\,1;\,\,2;\,\,...;\,\,48} \right\},\) tập hợp này có 49 phần tử.

Đáp án đúng là: A

Gọi \[a{\rm{\;(m)}}\] là độ dài cạnh của nền kim tự tháp dạng hình vuông \[\left( {a > 0} \right)\].

Diện tích của nền kim tự tháp đó là \[{a^2}{\rm{(}}{{\rm{m}}^2}{\rm{)}}\]

Theo bài ra, ta có: \({a^2} = 53\,\,052\)

Suy ra \(a = \sqrt {53\,\,052} \approx 230,3\) (m).

Vậy độ dài cạnh của nền kim tự tháp đó là khoảng \[230,3{\rm{ m}}.\]

Đáp án đúng là: A

Vận tốc bay của một vật khi biết vật đó có khối lượng 3 kg và động năng 54 J là:

\[v = \sqrt {\frac{{2 \cdot 54}}{3}} = \sqrt {\frac{{108}}{3}} = \sqrt {36} = 6\,\,({\rm{m/s}}).\]

Vậy vận tốc bay của vật đó là 6 m/s.