II. Thông hiểu
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 10{\rm{\;cm}},\,\,\widehat C = 30^\circ .\] Độ dài cạnh \[AB\] bằng
A. \[\frac{{5\sqrt 3 }}{3}\] (cm).
B. \[\frac{{10\sqrt 3 }}{3}\] (cm).
C. \[5\sqrt 3 \] (cm).
D. \[10\sqrt 3 \] (cm).
Giải bởi Vietjack
Đáp án đúng là: B
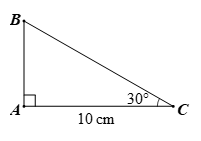
Vì tam giác \[ABC\] vuông tại \[A\] nên \[AB = AC.\tan C = 10.\tan 30^\circ = \frac{{10\sqrt 3 }}{3}\] (cm).
Do đó ta chọn phương án B.
Cho tam giác \[ABC\] vuông tại \[A\] có \[BC = 12{\rm{\;cm}},\,\,\widehat B = 40^\circ .\] Kết quả nào sau đây là đúng?
Cho tam giác \[ABC\] vuông tại \[A\] có \[BC = 15{\rm{\;cm}},\,\,AB = 12{\rm{\;cm}}.\] Kết quả nào sau đây là đúng?
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 20{\rm{\;cm}},\,\,\widehat {C\,} = 60^\circ .\] Độ dài cạnh \[BC\] bằng
Cho tam giác \[ABC\] vuông tại \[A\] có \[AB = 5{\rm{\;cm,}}\,\,AC = 7{\rm{\;cm}}{\rm{.}}\] Kết quả nào sau đây là đúng?
Cho tam giác \[ABC\] vuông tại \[A\] có \[AB = 6{\rm{\;cm}},\,\,\tan B = \frac{5}{{12}}.\] Kết quả nào sau đây là đúng?
Cho tam giác \[ABC\] vuông tại \[A\] có \[AC = 16{\rm{\;cm}},\,\,\sin B = \frac{3}{5}.\] Kết quả nào sau đây là sai?
III. Vận dụng
Cho tam giác \[ABC\] nhọn có \[AB = 3,5;\,\,AC = 4;\,\,\widehat {A\,} = 40^\circ \] và \[BH\] là đường cao. Diện tích tam giác \[ABC\] gần nhất với
Cho tam giác \[ABC\] có \[BC = 9{\rm{\;cm}},\,\,\widehat {ABC} = 50^\circ \] và \[\widehat {ACB} = 35^\circ .\] Gọi \[N\] là chân đường vuông góc hạ từ \[A\] xuống cạnh \[BC.\] Độ dài \[AN\] gần nhất với giá trị nào dưới đây?
Nếu tam giác \[MNP\] vuông tại \[M\] có \[NP = 5,\,\,\cos N = \frac{3}{5}\] thì \[MN\] bằng
Cho hình thang \[ABCD\] có \[\widehat {A\,} = \widehat {D\,} = 90^\circ ,\,\,\widehat {C\,} = 50^\circ .\] Biết rằng \[AB = 2;\,\,AD = 1,2.\] Khi đó diện tích hình thang \[ABCD\] gần nhất với
