8 câu hỏi trắc nghiệm thuộc Dạng 4: Góc có đỉnh ở bên trong hay bên ngoài đường tròn có đáp án

Câu 1:

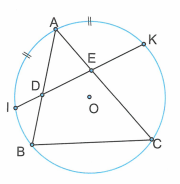
Cho tam giác ABC nội tiếp trong đường tròn (O). Trên các cung nhỏ AB và AC lần lượt lấy các điểm I và K sao cho $\overset{⏜}{I A} = \overset{⏜}{A K}$ . Dây IK cắt các cạnh AB, AC lần lượt tại D và E.

a) Chứng minh rằng $\hat{A D K} = \hat{A C B}$ .

Xem đáp án

a) Ta thấy $\hat{A D K}$ là góc có đỉnh D nằm trong đường tròn $(O)$ nên:

$\hat{A D K} = \frac{1}{2} (s đ \overset{⏜}{A K} + s đ \overset{⏜}{I B}) = \frac{1}{2} (s đ \overset{⏜}{A I} + s đ \overset{⏜}{I B}) = \frac{1}{2} s đ \overset{⏜}{A B}$ . (1)

Mà $\hat{A C B}$ là góc nội tiếp chắn cung $\overset{⏜}{A B}$ nên: $\hat{A C B} = \frac{1}{2} s đ \overset{⏜}{A B}$ . (2)

Từ (1) và (2) suy ra $\hat{A D K} = \hat{A C B}$ .

Câu 2:

b) Tam giác ABC phải có thêm điều kiện gì thì tứ giác DECB là hình thang cân.

Xem đáp án

b) Tứ giác DECB là hình thang cân

$\Leftrightarrow D E C B$ là hình thang và $\hat{C} = \hat{B}$

$\Leftrightarrow \{\begin{cases} D E // B C \\ \hat{C} = \hat{B} \end{cases} \Leftrightarrow \{\begin{cases} \hat{A D E} = \hat{A B C} \\ \hat{C} = \hat{B} \end{cases} \Leftrightarrow \hat{C} = \hat{B} \Leftrightarrow Δ A B C$ cân tại A.

Vậy tam giác ABC phải là tam giác cân tại A thì tứ giác DECB là hình thang cân.

Câu 3:

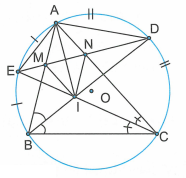
Cho tam giác ABC nội tiếp trong đường tròn (O). Các tia phân giác của góc B và góc C cắt nhau tại I và cắt đường tròn (O) lần lượt tại D và E. Dây DE cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh rằng:

a) Tam giác AMN là tam giác cân.

Xem đáp án

a) Theo giả thiết BD là tia phân giác của góc $\hat{A B C}$ nên D là điểm chính giữa của cung $\overset{⏜}{A C} \Rightarrow \overset{⏜}{D A} = \overset{⏜}{D C}$ . (1)

Tương tự ta cũng có E là điểm chính giữa của cung $\overset{⏜}{A B}$

$\Rightarrow \overset{⏜}{E A} = \overset{⏜}{E B}$ . (2)

Góc $\hat{A M N}$ và $\hat{A N M}$ là hai góc có đỉnh nằm trong đường tròn (O) nên:

$s đ \hat{A M N} = \frac{1}{2} (s đ \overset{⏜}{A D} + s đ \overset{⏜}{E B})$ và $s đ \hat{A N M} = \frac{1}{2} (s đ \overset{⏜}{D C} + s đ \overset{⏜}{E A})$ . (3)

Từ (1), (2) và (3) suy ra $\hat{A M N} = \hat{A N M} \Rightarrow Δ A M N$ cân tại A.

Câu 4:

b) Các tam giác EAI và DAI là những tam giác cân.

Xem đáp án

b) Ta có $\hat{E A I} = \hat{E A B} + \hat{B A I}; \hat{A I E} = \hat{I C A} + \hat{I A C}$ (góc ngoài của tam giác AIC). (4)

$\hat{E A B} = \hat{E C A}$ (hai góc nội tiếp cùng chắn hai cung bằng nhau là $\overset{⏜}{E B}, \overset{⏜}{E A}$ ). (5)

Vì I giao điểm hai đường phân giác của $Δ A B C$ , suy ra AI là đường phân giác của góc $\hat{B A C}$

$\Rightarrow \hat{B A I} = \hat{C A I}$ . (6)

Từ (4), (5) và (6) suy ra $\hat{E A I} = \hat{E I A} \Rightarrow Δ E A I$ cân tại E.

Chứng minh hoàn toàn tương tự, ta cũng có $\hat{I A D} = \hat{A I D} \Rightarrow Δ A I D$ cân tại D.

Câu 5:

c) Tứ giác AMIN là hình thoi.

Xem đáp án

c) Vì AI là đường phân giác của $Δ A M N$ cân tại A nên AI vuông góc với MN tại trung điểm của MN.

Tương tự, $Δ D A I$ cân tại D nên MN vuông góc với AI tại trung điểm của AI.

Do đó AMIN là hình thoi vì có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.

Câu 6:

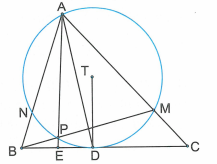
Trong tam giác ABC, đường phân giác của $\hat{B A C}$ cắt cạnh BC tại D. Giả sử (T) là đường tròn tiếp xúc với BC tại và đi qua điểm D. Gọi M là giao điểm thứ hai của (T) và AC, P là giao điểm thứ hai của (T) và BM, E là giao điểm của AP và BC.

a) Chứng minh rằng $\hat{E A B} = \hat{M B C}$ .

Xem đáp án

a) Gọi N là giao điểm thứ hai của AB với đường tròn (T).

Do AD là phân giác của $\hat{B A C} \Rightarrow \overset{⏜}{N D} = \overset{⏜}{M D}$ .

Ta có $\hat{M B C} = \frac{1}{2} (s đ \overset{⏜}{D M} - s đ \overset{⏜}{D P}) = \frac{1}{2} (s đ \overset{⏜}{D N} - s đ \overset{⏜}{D P}) = \frac{1}{2} s đ \overset{⏜}{N P} = \hat{E A N}$ .

$\Rightarrow \hat{M B C} = \hat{E A B}$ (đpcm).

Câu 7:

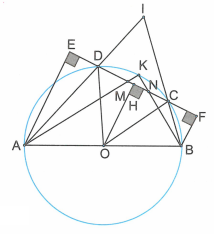
Cho bốn điểm A,D,C,B theo thứ tự đó nằm trên đường tròn tâm O đường kính AB=2R. Gọi E và F theo thứ tự là hình chiếu vuông góc của A,B trên đường thẳng CDA. Tia AD cắt tia BC tại I. Biết $A E + B F = R \sqrt{3}$ .

a) Tính số đo $\hat{A I B}$ .

Xem đáp án

a) Kẻ $O H ⊥ C D (H \in C D)$ , ta thấy OH là đường trung bình của hình thang ABFE, suy ra

$O H = \frac{1}{2} (A E + B F) = \frac{R \sqrt{3}}{2}$ .

Tam giác vuông DOH có: $\sin \hat{O D H} = \frac{O H}{O D} = \frac{R \sqrt{3}}{2 R} = \frac{\sqrt{3}}{2} \Rightarrow \hat{O D H} = 60 °$ .

Do đó tam giác $O C D$ đều, suy ra $\hat{C O D} = 60 ° \Rightarrow s đ \overset{⏜}{C K D} = 60 °$ .

Ta thấy $\hat{A I B}$ có đỉnh nằm ngoài đường tròn (O) nên:

$\hat{A I B} = \frac{1}{2} (s đ \overset{⏜}{A B} - s đ \overset{⏜}{C K D}) = \frac{1}{2} (180 ° - 60 °) = 60 °$ .

Câu 8:

b) Trên cung nhỏ CD lấy điểm K. Gọi giao điểm của KA,KB với DC lần lượt là M và N. Tìm giá trị lớn nhất của MN khi K di động trên cung nhỏ CD.

Xem đáp án

b) Ta có: $\hat{M K N} = 90 °$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow \hat{K M N} + \hat{K N M} = 90 °$ . (1)

Trong tam giác vuông EMA có: $\hat{E A M} + \hat{E M A} = 90 °$ . (2)

Mà $\hat{K M N} = \hat{E M A}$ (đối đỉnh); $\hat{K M N} = \hat{B N F}$ (đối đỉnh). (3)

Từ (1), (2) và (3) suy ra $\hat{E A M} = \hat{B N F}$ .

Xét $Δ A E M$ và $Δ N F B$ có: $\hat{A E M} = \hat{B F C} = 90 °$ (giả thiết)

$\hat{E A M} = \hat{B N F}$ (chứng minh trên).

$\Rightarrow Δ A E M ~ Δ N F B (g.g) \Rightarrow \frac{E M}{F B} = \frac{A E}{N F} \Rightarrow E M . N F = A E . B F$ (không đổi).

Lại có: $M N = E F - (E M + N F)$ .

Do đó MN lớn nhất khi và chỉ khi EM+NF nhỏ nhất.

Áp dụng bất đẳng thức Cô-si ta có: $E M + N F \geq 2 \sqrt{E M . N F} = 2 \sqrt{A E . B F}$ .

Đẳng thức xảy ra khi $E M = F N = \sqrt{A E . B F}$ .

Vậy giá trị lớn nhất của MN bằng $E F - 2 \sqrt{A E . B F}$ .