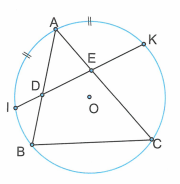
Cho tam giác ABC nội tiếp trong đường tròn (O). Trên các cung nhỏ AB và AC lần lượt lấy các điểm I và K sao cho . Dây IK cắt các cạnh AB, AC lần lượt tại D và E.
a) Chứng minh rằng .
Giải bởi Vietjack
a) Ta thấy là góc có đỉnh D nằm trong đường tròn nên:
. (1)
Mà là góc nội tiếp chắn cung nên: . (2)
Từ (1) và (2) suy ra .
Trong tam giác ABC, đường phân giác của cắt cạnh BC tại D. Giả sử (T) là đường tròn tiếp xúc với BC tại 
và đi qua điểm D. Gọi M là giao điểm thứ hai của (T) và AC, P là giao điểm thứ hai của (T) và BM, E là giao điểm của AP và BC.
a) Chứng minh rằng .
b) Trên cung nhỏ CD lấy điểm K. Gọi giao điểm của KA,KB với DC lần lượt là M và N. Tìm giá trị lớn nhất của MN khi K di động trên cung nhỏ CD.
b) Tam giác ABC phải có thêm điều kiện gì thì tứ giác DECB là hình thang cân.
Cho tam giác ABC nội tiếp trong đường tròn (O). Các tia phân giác của góc B và góc C cắt nhau tại I và cắt đường tròn (O) lần lượt tại D và E. Dây DE cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh rằng:
a) Tam giác AMN là tam giác cân.
Cho bốn điểm A,D,C,B theo thứ tự đó nằm trên đường tròn tâm O đường kính AB=2R. Gọi E và F theo thứ tự là hình chiếu vuông góc của A,B trên đường thẳng CDA. Tia AD cắt tia BC tại I. Biết .
a) Tính số đo .
