Để chuẩn bị cho buổi liên hoan của gia đình, bác Thu mua hai loại thực phẩm là thịt bò và thịt lợn. Giá tiền thịt bò là 250 nghìn đồng/kg, giá tiền thịt lợn là 150 nghìn đồng/kg. Bác Ngọc đã chi 500 nghìn để mua \[3,5\] kg hai loại thực phẩm trên. Gọi \[x\] và \[y\] lần lượt là số kilôgam thịt bò và thịt lợn mà bác Thu đã mua. Hệ phương trình bậc nhất hai ẩn biểu diễn mối quan hệ giữa \[x\] và \[y\] là
A. \[\left\{ \begin{array}{l}x + y = 3,5\\x + 150y = 500\end{array} \right.\].
B. \[\left\{ \begin{array}{l}x + y = 3,5\\250x + 150y = 500\end{array} \right.\].
C. \[\left\{ \begin{array}{l}x + y = 3,5\\250x + y = 500\end{array} \right.\].
D. \[\left\{ \begin{array}{l}x - y = 3,5\\250x + 150y = 500\end{array} \right.\].
Giải bởi Vietjack
Đáp án đúng là: B
Theo bài, bác Thu chỉ mua \[3,5\] kg thịt bò và thịt lợn nên ta có phương trình: \(x + y = 3,5\).
Do giá tiền thịt bò là 250 nghìn đồng/kg nên số tiền bác Thu chi ra để mua \(x\) kilôgam thịt bò là: \(250x\) (nghìn đồng).
Do giá tiền thịt lợn là 150 nghìn đồng/kg nên số tiền bác Thu chi ra để mua \(y\) kilôgam thịt lợn là: \(150y\) (nghìn đồng).
Theo bài, bác Thu đã chi 500 nghìn để mua hai loại thực phẩm trên nên ta có phương trình:
\(250x + 150y = 500\).
Vậy ta có hệ phương trình \[\left\{ \begin{array}{l}x + y = 3,5\\250x + 150y = 500\end{array} \right.\].
I. Nhận biết
Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất hai ẩn?
Tất cả các nghiệm của phương trình \(2x - 3y = 1\) được biểu diễn bằng đường thẳng nào dưới đây?
Tất cả các nghiệm của phương trình \(3x - 0y = 1\) được biểu diễn bởi
Giá trị nào của \[{x_0}\] để cặp số \(\left( {{x_0};\,\,2} \right)\) là nghiệm của phương trình \(2x + y = - 6\)?
Để chuẩn bị cho buổi liên hoan của gia đình, bác Thu mua hai loại thực phẩm là thịt bò và thịt lợn. Giá tiền thịt bò là 250 nghìn đồng/kg, giá tiền thịt lợn là 150 nghìn đồng/kg. Bác Ngọc đã chi 500 nghìn để mua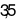 
kg hai loại thực phẩm trên. Gọi 
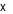và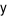 
lần lượt là số kilôgam thịt bò và thịt lợn mà bác Thu đã mua. Hệ phương trình bậc nhất hai ẩn biểu diễn mối quan hệ giữa 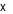và là
Hệ số \(a,\,\,b,\,\,c\) tương ứng của phương trình bậc nhất hai ẩn \(x + 2y - 1 = 0\) là
Cho hệ phương trình \[\left\{ \begin{array}{l}x + y = 0\\x + 3y = 4\end{array} \right.\], cặp số nào sau đây là nghiệm của hệ phương trình đã cho?
Giá trị nào của \[{y_0}\] để cặp số \(\left( {1;\,\,{y_0}} \right)\) là nghiệm của phương trình \( - 3x + 2y = 7\)?
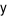Biết phương trình \[mx - 5y + 1 = 0\] nhận cặp số \[\left( {1;2} \right)\] làm nghiệm. Giá trị của \[m\] là
Cho phương trình \[3x + \left( {{m^2} + m} \right)y = 6\] có nghiệm \[\left( { - 2;6} \right)\]. Có bao nhiêu giá trị \(m\) thỏa mãn điều kiện trên?
Trong các hệ phương trình sau, hệ nào không phải là hệ phương trình bậc nhất hai ẩn?
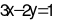luôn nhận cặp số nào sau đây là nghiệm khi 
thay đổi?
?
nhận cặp số 
làm nghiệm. Giá trị của 
là
