Nước từ vòi phun nước (đặt cách mặt nước \[0,2{\rm{ m)}}\] được phun lên cao sẽ đạt một độ cao nào đó rồi rơi xuống. Giả sử nước được từ đầu vòi phun (vị trí \[A)\] và rơi xuống vị trí \(B.\) Đường đi của nước là một phần của parabol dạng \(y = - \frac{1}{8}{x^2}\) trong hệ trục tọa độ \[Oxy\] với \(O\) là điểm cao nhất của nước được phun ra so với mặt nước, trục \[Ox\] song song với \[AB,{\rm{ }}x\] và \(y\) tính bằng đơn vị mét. Biết \(AB = 12\;\,{\rm{m}}\,{\rm{.}}\) Tính chiều cao \(h\) từ điểm \(O\) đến mặt nước (Hình 5).
![Nước từ vòi phun nước (đặt cách mặt nước 0,2m được phun lên cao sẽ đạt một độ cao nào đó rồi rơi xuống. Giả sử nước được từ đầu vòi phun (vị trí A] và rơi (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid10-1728613927.png)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp số: \(4,7{\rm{\;m}}.\)
Đồ thị hàm số \(y = - \frac{1}{8}{x^2}\) đối xứng qua trục \(Oy,\) do đó \(A,\,\,B\) đối xứng với nhau qua trục \(Oy.\)
Gọi \(H\) là giao điểm của \[AB\] và \[Oy,\] khi đó ta có \(H\) là trung điểm của \(AB\) nên \[BH = \frac{1}{2}AB = 6{\rm{\;(m)}}{\rm{.}}\]
Thay \(x = 6\) vào hàm số \(y = - \frac{1}{8}{x^2}\), ta được \(y = - \frac{1}{8} \cdot {6^2} = - 4,5\).
Vậy chiều cao từ điểm \(O\) đến mặt nước là \[\left| { - 4,5} \right| + 0,2 = 4,7{\rm{\;(m)}}{\rm{.}}\]
Từ điểm M nằm ngoài đường tròn (O) kẻ hai tiếp tuyến MA, MB tới (O), (A, B là các tiếp điểm). Gọi H là giao điểm của AB với MO; E và F là các giao điểm của đường thẳng MO với đường tròn (O) (với ME < MF)
1) Chứng minh bốn điểm M, A, O, B cùng thuộc một đường tròn.
2) Chứng minh và HE.HF = HM.HO
3) Kẻ đường kính BP của đường tròn (O). Đường thẳng MP cắt đường tròn (O) tại điểm N (N khác P) Gọi I là trung điểm của đoạn thẳng MH. Chứng minh và ba điểm A, N, I thẳng hàng.
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Lúc 7 giờ sáng, một ca nô xuôi dòng sông từ bến A đến bến B dải 36 km. Khi đến bến B, ca nô nghỉ 30 phút. Sau đó, ca nô lại ngược dòng từ bến B về đến bến A lúc 10 giờ 48 phút cùng ngày. Tính vận tốc riêng của ca nô, biết vận tốc dòng nước là 2 km/h
Trong mặt phẳng với hệ tọa độ Oxy cho parabol và đường thẳng y = 5xx - m - 1 với m là tham số.
a) Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt.
b) Tìm tất cả các giá trị của m đề (d) cắt (P) tại hai điểm phân biệt có hoành độ là các số tự nhiên.
Một quả bóng đá tiêu chuẩn thường được sử dụng tại các giải thi đấu có diện tích bề mặt là Coi quả bóng đá có dạng hình cầu, tính thể tích của quả bóng (làm tròn kết quả đến một chữ số thập phân và lấy
Cho hai biểu thức:
và với
1) Tính giá trị của biểu thức B khi x = 49
2) Rút gọn biểu thức A
3) Tìm tất cả các giá trị của x để P = AB có giá trị là một số nguyên.
Một hộp chứa 15 quả cầu màu xanh được đánh số từ 1 đến 15 và 5 quả cầu màu đỏ được đánh số từ 16 đến 20. Lấy ngẫu nhiên một quả cầu trong hộp.
a) Xác suất để lấy được quả cầu màu xanh bằng xác suất để lấy được quả cầu màu đỏ.
b) Xác suất để lấy được quả cầu ghi số chẵn là \[0,5.\]
c) Xác suất để lấy ra quả cầu có màu xanh và ghi số lẻ là \[0,4.\]
Một trường trung học cơ sở mua 500 quyển vở bao gồm \(x\) quyển vở loại thứ nhất và \(y\) quyển vở loại thứ hai \(\left( {x,y \in \mathbb{N}*} \right)\) để làm phần thưởng cho học sinh. Giá bán của mỗi quyển vở loại thứ nhất, loại thứ hai lần lượt là \[8\,\,000\] đồng và \[9\,\,000\] đồng. Biết tổng số tiền nhà trường đã dùng để mua 500 quyển vở đó là \[4\,\,200\,\,000\] đồng. Mỗi học sinh Xuất sắc được thưởng 02 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai; mỗi học sinh Giỏi được thưởng 01 quyển vở loại thứ nhất và 01 quyển vở loại thứ hai; các học sinh khác không được thưởng và số học sinh này chiếm \(40\% \) tổng số học sinh cả trường.
a) \(x + y = 500\).
b) \(9x + 8y = 4\,\,200\,\,000\).
c) \(x = 300;y = 200\).
Một chiếc áo có giá niêm yết là \[120\,\,000\] đồng. Để thanh lí chiếc áo, đầu tiên người ta giảm giá \(x\% \) so với giá niêm yết. Do vẫn chưa bán được chiếc áo nên người ta tiếp tục giảm giá \(x\% \) so với giá vừa được giảm. Sau hai đợt giảm giá, giá của chiếc áo còn \[76\,\,800\] đồng.
a) Giá của chiếc áo sau lần giảm giá thứ nhất là: \(120\,\,000 - 1200x\) (đồng).
b) Giá của chiếc áo sau hai lần giảm giá là: \(12{x^2} - 2\,\,400x + 120\,\,000\) (đồng).
c) Theo bài, sau hai đợt giảm giá, giá của chiếc áo còn \[76\,\,800\] đồng nên ta có phương trình \({x^2} - 200x + 3\,\,600 = 0\).
d) \(x = 180\).
Người ta muốn dựng một khung cổng hình vuông \[ABCD\] có độ dài cạnh bằng \[3{\rm{ cm}}\] được bao bởi một khung thép có dạng nửa đường tròn tâm \(F\) bán kính \[FA\] (như hình 3).
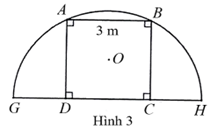
a) Độ dài đoạn thẳng \[OA\] là \(1,5\sqrt 2 \;\,{\rm{m}}\).
b) Độ dài đoạn thẳng \(HG = 3\sqrt 5 \;\,{\rm{m}}\).
c) Độ dài cung \[GAH\] là \(3\sqrt 5 \pi \,\,{\rm{m}}\).
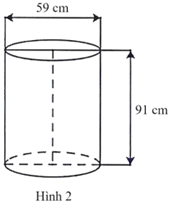
(Đơn vị tính: Đồng. Lấy \(\pi \approx 3,14,\) làm tròn kết quả đến hàng nghìn).