III. Vận dụng
Hình vẽ dưới đây mô tả vị trí tương đối giữa mỗi cặp đường tròn trong hình chụp bộ cồng chiêng Tây Nguyên:

Hai đường tròn của cặp cồng chiêng ở hình nào tiếp xúc trong với nhau?
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Không có hình nào biểu diễn cặp cồng chiêng có hai đường tròn tiếp xúc trong với nhau.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Cặp đường tròn ở cặp cồng chiêng trong Hình 1 không có điểm chung nên cặp đường tròn này không giao nhau.
Cặp đường tròn ở cặp cồng chiêng trong Hình 2 có một điểm chung và không có cồng chiêng nào treo trước cồng chiêng còn lại nên cặp đường tròn này tiếp xúc ngoài với nhau.
Cặp đường tròn ở cặp cồng chiêng trong Hình 3 có hai điểm chung nên cặp đường tròn này cắt nhau tại hai điểm phân biệt.
Vậy không có hình nào biểu diễn cặp cồng chiêng có hai đường tròn tiếp xúc trong với nhau.
Do đó ta chọn phương án D.
Cho hai đường tròn đồng tâm \[\left( {O;2{\rm{\;cm}}} \right)\] và \[\left( {O;3{\rm{\;cm}}} \right).\]
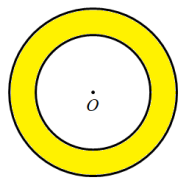
Diện tích hình vành khuyên được giới hạn bởi hai đường tròn đó là
Một họa tiết trang trí có dạng hình tròn bán kính \[5{\rm{\;dm}}\] được chia thành nhiều hình quạt tròn (hình vẽ), mỗi hình quạt tròn có góc ở tâm là \[7,5^\circ .\]

Diện tích tất cả các hình quạt tròn được tô màu ở hình vẽ trên là bao nhiêu đề-xi-mét vuông (làm tròn kết quả đến hàng phần trăm)?
Nếu đường thẳng \[d\] là tiếp tuyến của đường tròn \[\left( O \right)\] tại \[A\] thì
I. Nhận biết
Cho đường tròn \[\left( {O;\,2{\rm{\;cm}}} \right)\] và một điểm \[H\] bất kì. Nếu \[OH < 2{\rm{\;cm}}\] thì
Cho hình vuông \(ABCD\) cạnh bằng \(2{\rm{\;cm}}.\) Gọi \(I,\,\,J\) lần lượt là trung điểm của \(AC,\,\,CD.\) Vị trí tương đối của đường tròn \(\left( {A;\,AI} \right)\) và \(\left( {C;\,CJ} \right)\) là
II. Thông hiểu
Hai tiếp tuyến tại \(B\) và \(C\) của đường tròn \((O)\) cắt nhau tại \(A\). Khẳng định nào sau đây là sai?
Cho đường tròn \[\left( O \right)\] bán kính \[OA.\] Từ trung điểm \[M\] của \[OA\] vẽ dây \[BC \bot OA.\] Biết độ dài đường tròn \[\left( O \right)\] là \[4\pi {\rm{\;cm}}.\] Độ dài cung lớn \[BC\] là
Cho hai đường tròn \[\left( {O;R} \right),\,\,\left( {O';R'} \right)\] cắt nhau tại \[A,\,\,B,\] trong đó \[O' \in \left( O \right).\] Kẻ đường kính \[O'C\] của \[\left( O \right).\] Khẳng định nào sau đây là đúng nhất?
Cho đường tròn \[\left( {O;R} \right).\] Từ một điểm \[M\] nằm ngoài đường tròn kẻ các tiếp tuyến \[ME,MF\] đến đường tròn (với \[E,F\] là các tiếp điểm). Đoạn \[OM\] cắt đường tròn \[\left( O \right)\] tại \[I.\] Kẻ đường kính \[ED\] của đường tròn \[\left( O \right).\] Hạ \[FK\] vuông góc với \[ED.\] Gọi \[P\] là giao điểm của \[MD\] và \[FK.\] Cho \[FK = 6{\rm{\;cm}}\] và các khẳng định sau:
(i) Các điểm \[M,E,O,F\] cùng thuộc một đường tròn.
(ii) \[FP = PK = 3{\rm{\;cm}}.\]
“Trong các dây của một đường tròn, đường kính là dây có độ dài …”. Cụm từ thích hợp điền vào chỗ trống là
Cho đường tròn \[\left( {O;OA} \right)\] và đường tròn \[\left( {O'} \right)\] đường kính \[OA.\] Vị trí tương đối của hai đường tròn\[\left( O \right)\] và \[\left( {O'} \right)\] là
Cho hình chữ nhật \[ABCD\] có \[AD = 8{\rm{\;cm}},\,\,AB = 15{\rm{\;cm}}.\] Biết rằng bốn điểm \[A,B,C,D\] cùng thuộc một đường tròn. Bán kính của đường tròn đó bằng
Cho đường tròn \[\left( {O;R} \right)\] và dây \[AB = R.\] Trên tia đối của tia \[BA\] lấy điểm \[C\] sao cho \[BC = BA.\] Kéo dài \[CO\] cắt đường tròn \[\left( O \right)\] lần lượt tại \[D,E\] (\[D\] nằm giữa \[C,O\]). Kết luận nào sau đây là sai?
Cho đường tròn tâm \(O\) và điểm \(A\) nằm ngoài đường tròn. Từ \(A\) kẻ hai tiếp tiếp tuyến \(AB\) và \(AC\) của đường tròn tâm \(O\) (điểm \(B,C\) là tiếp điểm). Nếu \(\widehat {BAC} = 90^\circ \) thì tam giác \(ABO\) là