Cho hình vẽ dưới đây:
![Cho hình vẽ dưới đây:Số đo góc \[ABC\] là (ảnh 1)](https://video.vietjack.com/upload2/images/1731491184/1731491902-image10.png)
Số đo góc \[ABC\] là
A. \(80^\circ \).
B. \(90^\circ \).
C. \(100^\circ \).
D. \(110^\circ \).
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh)
Đặt \(\widehat {BCE} = \widehat {DCF} = x\).
Theo tính chất góc ngoài tam giác, ta có:
\(\widehat {ABC} = \widehat {BCE} + \widehat E = x + 40^\circ \)
\(\widehat {ADC} = \widehat {DCF} + \widehat F = x + 20^\circ \)
Lại có \(\widehat {ABC} + \widehat {ADC} = 180^\circ \) (hai góc đối diện của tứ giác nội tiếp)
Suy ra \(\left( {x + 40^\circ } \right) + \left( {x + 20^\circ } \right) = 180^\circ \) hay \(x = 60^\circ \).
Do đó \(\widehat {ABC} = 60^\circ + 40^\circ = 100^\circ \).
Cho nửa đường tròn tâm \[O\], đường kính \[AB = 2R\]. Trên tia đối của tia \[AB\] lấy điểm \[E\] (khác với điểm \[A\]). Tiếp tuyến kẻ từ điểm \[E\] cắt các tiếp tuyến kẻ từ điểm \[A\] và \[B\] của nửa đường tròn \[\left( O \right)\] lần lượt tại \[C\] và \[D\]. Gọi \[M\] là tiếp điểm của tiếp tuyến kẻ từ điểm \[E\]. Trong các khẳng định sau, khẳng định nào là sai?
Cho điểm \[A\] nằm ngoài đường tròn \[\left( O \right)\] qua \[A\] kẻ hai tiếp tuyến \[AB\] và \[AC\] với đường tròn (\[B,{\rm{ }}C\] là tiếp điểm). Chọn đáp án đúng:
Cho tam giác \[ABC\] có hai đường cao \[BD\] và \[CE\] cắt nhau tại \[H\]. Trong các tứ giác sau, tứ giác nội tiếp là
I. Nhận biết
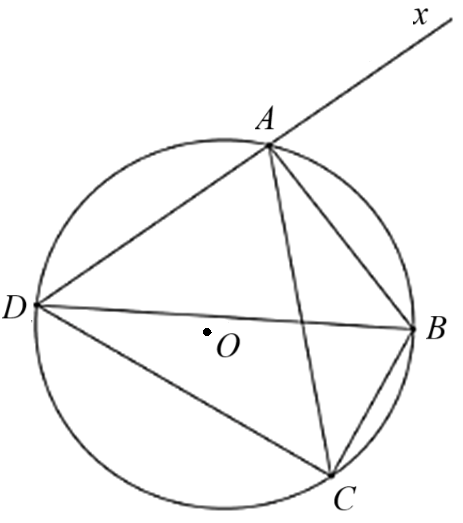
Cho tứ giác \[ABCD\] nội tiếp đường tròn \[\left( O \right)\]. Khẳng định nào sau đây là sai?
Cho nửa đường tròn \[\left( {O;{\rm{ }}R} \right)\] đường kính \[BC\]. Lấy điểm \[A\] trên tia đối của tia \[CB\]. Kẻ tiếp tuyến \[AF,{\rm{ }}Bx\] của nửa kia đường tròn \[\left( O \right)\] (với \[F\] là tiếp điểm). Tia \[AF\] cắt tia \[Bx\] của nửa đường tròn tại \[D\]. Khi đó tứ giác \[OBDF\] là
II. Thông hiểu
Cho đường tròn \[\left( O \right)\] có \[AB\] là đường kính. Trên tia đối của tia \[AB\] lấy điểm \[C\] nằm ngoài đường tròn. Lấy điểm \[M\] bất kì nằm trên đường tròn \[\left( O \right)\]. Gọi \[P\] là giao điểm của \[MB\] và đường vuông góc với \[AB\] tại \[C\]. Chọn khẳng định đúng.
Cho tứ giác \[ABCD\] có số đo các góc \[A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\] tương ứng. Trường hợp nào sau đây thì tứ giác \[ABCD\] có thể là tứ giác nội tiếp?
Trong các hình dưới đây.
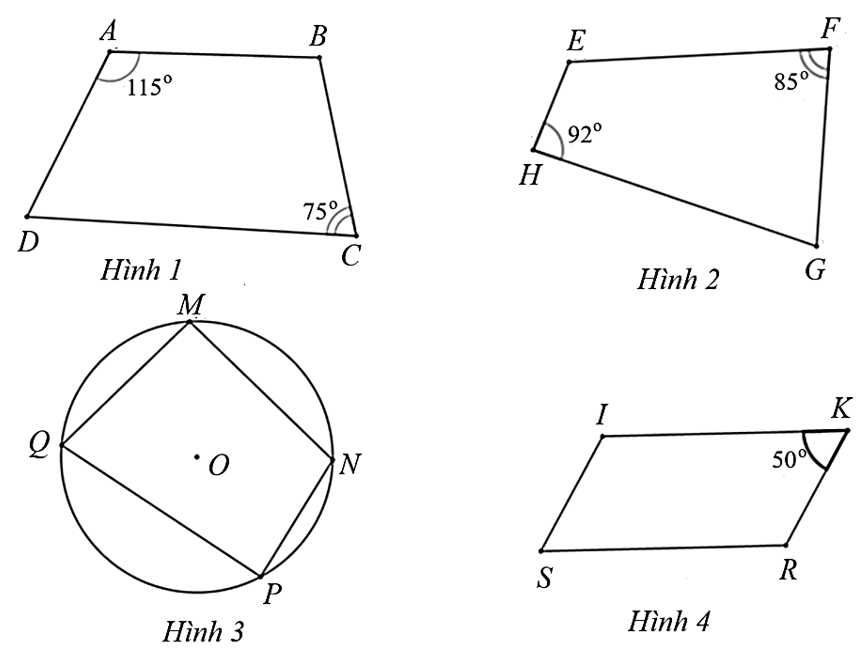
Trong các hình trên, tứ giác trong hình nào là tứ giác nội tiếp?
Cho tam giác \[ABC\] vuông tại \[A\] đường cao \[AH\]. Kẻ \[HE\] vuông góc với \[AB\] tại \[E\], kẻ \[HF\] vuông góc với \[AC\] tại \[F\]. Chọn câu đúng:
Cho đường tròn \[\left( O \right)\] đường kính \[AB\]. Gọi \[H\] là điểm nằm giữa \[O\] và \[B\]. Kẻ dây \[CD\] vuông góc với \[AB\] tại \[H\]. Trên cung nhỏ \[AC\] lấy điểm \[E\], kẻ \[CK \bot AE\] tại K. Đường thẳng \[DE\] cắt \[CK\] tại \[F\]. Tích \[AH.{\rm{ }}AB\] bằng
III. Vận dụng
Cho đường tròn \[\left( O \right)\] đường kính \[AB\]. Gọi \[H\] là điểm nằm giữa \[O\] và \[B\]. Kẻ dây \[CD\] vuông góc với \[AB\] tại \[H\]. Trên cung nhỏ \[AC\] lấy điểm \[E\], kẻ \[CK \bot AE\] tại \[K\]. Đường thẳng \[DE\] cắt \[CK\] tại \[F\]. Tam giác \[ACF\] là tam giác
Cho hình bình hành \[ABCD\]. Đường tròn đi qua ba đỉnh \[A,{\rm{ }}B,{\rm{ }}C\] cắt đường thẳng \[CD\] tại \[P\] (điểm \[P\] khác với điểm \[C\]). Khi đó
Tứ giác \[ABCD\] nội tiếp đường tròn có hai cạnh đối \[AB\] và \[CD\] cắt nhau tại \[M\] và \(\widehat {BAD} = 70^\circ \) thì số đo góc \[BCM\] là