Cho hình trụ nằm bên trong hình lập phương có cạnh bằng \[x\] (hình vẽ).
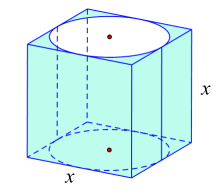
Tỉ số thể tích của hình trụ và hình lập phương đã cho là
A. \[\frac{\pi }{2}.\]
B. \[\frac{\pi }{4}.\]
C. \[\frac{\pi }{{12}}.\]
D. \[\frac{{2\pi }}{3}.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Quan sát hình vẽ, ta thấy:
⦁ Chiều cao của hình trụ bằng cạnh của hình lập phương. Tức là, \[h = x.\]
⦁ Đường kính đáy của hình trụ bằng cạnh của hình lập phương. Tức là, \[2r = x.\] Suy ra \[r = \frac{x}{2}.\]
Thể tích của hình trụ là: \[V = \pi {r^2}h = \pi \cdot {\left( {\frac{x}{2}} \right)^2} \cdot x = \frac{{\pi {x^3}}}{4}.\]
Thể tích của hình lập phương là: \[V' = {x^3}.\]
Do đó tỉ số thể tích của hình trụ và hình lập phương đã cho là: \[\frac{V}{{V'}} = \frac{{\frac{{\pi {x^3}}}{4}}}{{{x^3}}} = \frac{\pi }{4}.\]
Vậy ta chọn phương án B.
I. Nhận biết
Hình chữ nhật có chiều dài \[8{\rm{\;cm}},\] chiều rộng \[6{\rm{\;cm}}.\] Quay hình chữ nhật đó một vòng quanh chiều dài của nó ta được một hình trụ có chiều cao \[h\] và bán kính đáy \[r.\]
Kết luận nào sau đây là đúng?
II. Thông hiểu
Một hình trụ có đường kính đáy \[2{\rm{\;dm}},\] đường sinh \[14{\rm{\;dm}}.\] Thể tích của hình trụ đó bằng
Nếu tăng bán kính đáy của hình trụ lên 4 lần và giữ nguyên chiều cao thì thể tích mới của hình trụ
Gọi \[l,h,r\] lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ \[\left( T \right).\] Diện tích xung quanh \[{S_{xq}}\] của hình trụ \[\left( T \right)\] có công thức là
Cho hình chữ nhật có chiều dài \[10{\rm{\;cm}},\] chiều rộng \[7{\rm{\;cm}}.\] Quay hình chữ nhật đó một vòng quanh chiều dài của nó ta được một hình trụ có thể tích bằng
Cho hình trụ có chiều cao \[h = 12{\rm{\;cm}}\] và diện tích xung quanh \[{S_{xq}} = 64\pi {\rm{\;c}}{{\rm{m}}^2}.\] Bán kính đáy của hình trụ là
Gọi \[l,h,r\] lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ \[\left( T \right).\] Diện tích toàn phần \[{S_{tp}}\] của hình trụ \[\left( T \right)\] có công thức là
Cho hình chữ nhật có chiều dài \[3{\rm{\;cm}},\] chiều rộng \[2{\rm{\;cm}}.\] Quay hình chữ nhật đó một vòng quanh chiều dài của nó ta được một hình trụ có diện tích xung quanh bằng
Cho hình chữ nhật \[MNPQ\] có \[MN = 16{\rm{\;cm}},NP = 12{\rm{\;cm}}.\] Khi quay hình chữ nhật đã cho một vòng quanh cạnh \[MN\] ta được một hình trụ có diện tích toàn phần (lấy \[\pi \approx 3,14)\] khoảng
Gọi \[h,\,\,r\] lần lượt là chiều cao và bán kính đáy của hình trụ \[\left( T \right).\] Thể tích \[V\] của hình trụ \[\left( T \right)\] có công thức là
Cho hình trụ có bán kính đáy \[r = 8{\rm{\;cm}}\] và diện tích toàn phần \[564\pi {\rm{\;c}}{{\rm{m}}^2}.\] Chiều cao của hình trụ bằng
Một ống nước có dạng hình trụ (như hình vẽ).
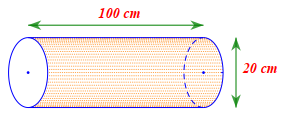
Kết luận nào sau đây là đúng?
Một hình trụ \[\left( T \right)\] được tạo ra khi quay hình chữ nhật \[ABCD\] một vòng quanh cạnh \[AB.\] Biết \[AC = 2a\sqrt 2 \] và \[\widehat {ACB} = 45^\circ .\] Thể tích \[V\] của hình trụ \[\left( T \right)\] là
III. Vận dụng
Một hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \[h = 12{\rm{\;cm}}\] và đường kính đáy \[d = 8{\rm{\;cm}}.\] Diện tích toàn phần của hộp sữa là