Tam giác \(ABC\) vuông tại \(A\) có \(AB = 4\,\,{\rm{cm}}\), \(AB = 3\,\,{\rm{cm}}\) nội tiếp nửa đường tròn tâm \(O\) đường kính \(BC\). Khi quay nửa hình tròn tâm \(O\) bán kính \(R\) quanh đường kính \(BC\) cố định ta thu được một hình cầu có bán kính là
A. \[2,5{\rm{\;cm}}.\]
B. \[3{\rm{\;cm}}.\]
C. \[4{\rm{\;cm}}.\]
D. \[5{\rm{\;cm}}.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
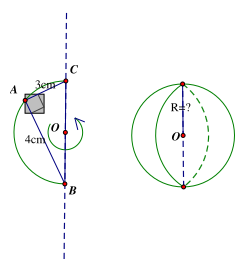
Khi quay nửa hình tròn tâm \(O\) quanh đường kính \(BC\) cố định ta thu được một hình cầu có đường kính \(BC\) và bán kính là \(R = \frac{{BC}}{2}\)
Áp dụng định lý Pythagore cho tam giác \(ABC\) vuông tại \(A,\) ta có:
\(B{C^2} = A{C^2} + A{B^2} = {3^2} + {4^2} = 25\)
Suy ra \(BC = \sqrt {25} = 5\) (do \(BC > 0).\)
Do đó \(R = \frac{{BC}}{2} = \frac{5}{2} = 2,5\) cm.
Vậy ta chọn phương án A.
Cho hình cầu có đường kính của đường tròn lớn là \[50{\rm{\;dm}}.\] Thể tích hình cầu đó bằng
Một quả bóng bi-a có dạng hình cầu, biết đường kính của nó bằng \[61{\rm{\;mm}}.\] Độ dài đường tròn lớn của quả bóng bi-a (lấy \[\pi \approx 3,14\]) khoảng
Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (như hình vẽ).
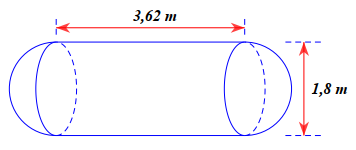
Thể tích của bồn chứa xăng là
Khi cắt hình cầu tâm \[O\] bán kính \[R\] bởi một mặt phẳng bất kỳ thì mặt cắt thu được luôn là một
Đường kính của một quả bóng tennis là \[2,63\,\,inch.\] Hỏi bề mặt của quả bóng tennis đó có diện tích khoảng bao nhiêu centimet vuông (kết quả làm tròn đến hàng phần mười và biết \[\pi \approx 3,14\], \[1\,\,inch \approx 2,54{\rm{\;cm}})?\]
III. Vận dụng
Một tháp nước có bể chứa là một hình cầu, bán kính phía trong đo được là \[6{\rm{\;m}}.\] Người ta dự tính lượng nước đựng đầy trong tháp đó đủ dùng cho một khu dân cư trong một ngày. Cho biết khu dân cư đó có \[6\,\,520\] người. Hỏi người ta đã dự tính mức bình quân mỗi người dùng bao nhiêu lít nước trong một ngày (lấy \[\pi \approx 3,14)?\]
I. Nhận biết
Hình cầu tâm \[O\] bán kính \[R\] được tạo ra khi quay
II. Thông hiểu
Hình cầu tâm \[O\] bán kính \[R\] có diện tích bề mặt bằng \[4\pi \,\,{{\rm{m}}^2}\] thì có bán kính \[R\] là
Một mặt cầu có đường kính \[d = 30{\rm{\;cm}}.\] Diện tích mặt cầu đó bằng
Một quả bóng khúc côn cầu có dạng hình cầu có độ dài đường tròn lớn là \[26\pi {\rm{\;cm}}.\] Thể tích của quả bóng đó (kết quả làm tròn đến hàng phần mười và lấy \[\pi \approx 3,14\]) khoảng
Bạn An bỏ một viên bi đặc hình cầu không thấm nước vào một lọ thủy tinh chứa nước dạng hình trụ có bán kính đường tròn đáy bằng \[8{\rm{\;cm}}.\] Biết rằng khi viên bi chìm hoàn toàn trong nước thì nước trong lọ dâng lên thêm \[2,25{\rm{\;cm}}\] và không bị tràn ra ngoài.
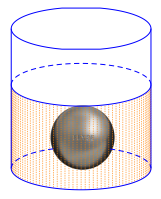
Lấy \[\pi \approx 3,14\] và xem độ dày của lo không đáng kể. Bán kính của viên bi bị bạn An đã bỏ vào lọ thủy tinh là