Có bao nhiêu số nguyên m để phương trình $9.3^{2x}-m\left(4\sqrt[4]{x^2+2x+1}+3m+3\right).3^x+1=0$ có đúng 3 nghiệm phân biệt?

Giả sử hàm f có đạo hàm cấp 2 trên R thỏa mãn $f\left(1\right)=f\text{'}\left(1\right)=1$ và $f\left(1-x\right)+x^{2}f\text{'}\text{'}\left(x\right)=2x, \forall x\in \mathrm{ℝ}$. Tính tích phân ${\int }_0^{1}xf\text{'}\left(x\right)dx$

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, $AC=a\sqrt{3}$, SAB là tam giác đều, $\widehat{SAD}=120°$. Tính thể tích của khối chóp S.ABCD

Cho cấp số cộng (u_n) có $u_1=-2, u_4=4$. Số hạng $u_6$ là

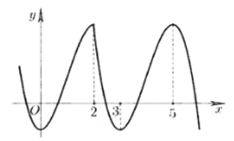
Cho số thực m và hàm số y = f(x) có đồ thị như hình vẽ bên. Phương trình $f\left(2^x+2^{-x}\right)$ có nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn [-1;2]?

Cho hàm số y = f(x) liên tục, nhận giá trị dương trên R và có bảng xét dấu đạo hàm như hình bên. Hàm số $y={\log }_x\left(f\left(2x\right)\right)$ đồng biến trên khoảng

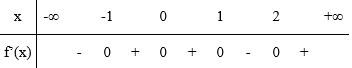
Trong không gian Oxyz, cho tam giác ABC vuông tại A, $\widehat{ABC}=30°, BC=3\sqrt{2}$, đường thẳng BC có phương trình $\frac{x-4}{1}=\frac{y-5}{1}=\frac{z+7}{-4}$, đường thẳng AB nằm trong mặt phẳng $\left(\alpha \right): x+z-3=0$. Biết đỉnh C có cao độ âm. Tính hoành độ của đỉnh A.

Tính đạo hàm của hàm số $y={\left(3x\right)}^e+{\log }_2\frac{1}{x}$

Cho các số phức z và w thỏa mãn $\left(2+i\right)\left|z\right|=\frac{z}{w}+1-i$. Tìm giá trị lớn nhất của $T=\left|w+1-i\right|$

Một biển quảng cáo có dạng hình Elip với bốn đỉnh $A_1, A_2, B_1, B_2$, như hình vẽ bên. Người ta chia Elip bởi Parabol có đỉnh B₁, trục đối xứng B₁B₂, và đi qua các điểm M ,N. Sau đó sơn phần tô đậm với giá 200.000 đồng/m² và trang trí đèn Led phần còn lại với giá 500.000 đồng/m². Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết rằng A₁A₂ = 4m, B₁B₂ = 2m, MN = 2m 

Tính thể tích V của vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 4, biết rằng khi cắt bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x(0 < x < 4) thì được thiết diện là nửa hình tròn có bán kính $R=x\sqrt{4-x}$

Cho hàm số y = f(x) có tập xác định và bảng biến thiên như hình vẽ

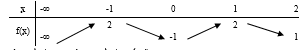
Mệnh đề nào sau đây sai về hàm số đã cho ?

Cho hình nón đỉnh S có đường sinh bằng 2, đường cao bằng 1. Tìm đường kính của mặt cầu chứa điểm S và chứa đường tròn đáy hình nón đã cho. 

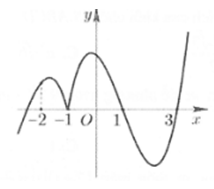
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Có bao nhiêu số nguyên m để bất phương trình $\left(mx+m^2\sqrt{5-x^2}+2m+1\right)f\left(x\right)\ge 0$ nghiệm đúng với mọi $x\in \left[-2;2\right]$?

Mệnh đề nào sau đây sai? 

Giả sử f(x) và g(x) là các hàm số bất kỳ liên tục trên và a, b, c là các số thực.

Mệnh đề nào sau đây sai?