Trong không gian Oxyz, cho điểm M(-3;9;6). Gọi $M_1, M_2, M_3$ lần lượt là hình chiếu vuông góc của M trên các trục tạo độ Ox, Oy, Oz. Mặt phẳng $\left(M_1{M}_2{M}_3\right)$ có phương trình là 

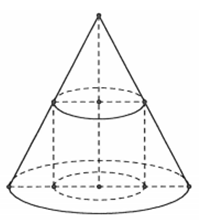
Cho hình nón có chiều cao 2R và bán kính đường tròn đáy R. Xét hình trụ nội tiếp hình nón sao cho thể tích khối trụ lớn nhất, khi đó bán kính đáy của khối trụ bằng

Cho hàm số f(x) xác định và có đạo hàm trên khoảng $\left(0;+\infty \right)$, đồng thời thỏa mãn điều kiện $f\left(1\right)=1+e, f\left(x\right)=e^{\frac{1}{x}}+x.f\text{'}\left(x\right), \forall x\in \left(0;+\infty \right)$. Giá trị của f(2) bằng

Nếu ${\log }_{2}3=a$ thì ${\log }_{72}108$ bằng

Cho khối cầu tâm O và bán kính R. Xét hai mặt phẳng (P), (Q) thay đổi song song với nhau có khoảng cách là R và cùng cắt khối cầu theo tiết diện là hai hình tròn. Tổng diện tích của hai hình tròn này có giá trị lớn nhất là 

Một vật chuyển động với vận tốc $v\left(t\right)=3t^2+4\left(m/s\right)$, trong đó t là khoảng thời gian tính bằng giây. Tính quãng đường vật đó đi được trong khoảng thời gian từ giây thứ 3 đến giây thứ 10?

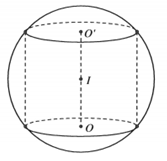
Cho khối cầu (S) có bán kính R. Một khối trụ có thể tích bằng $\frac{4\mathrm{\pi }\sqrt{3}}{9}{R}^3$ và nội tiếp khối cầu (S). Chiều cao khối trụ bằng

Số nghiệm dương của phương trình $\ln \left|x^2-5\right|=0$ là

Trong không gian Oxyz, cho hai mặt phẳng $\left(P\right): 2x-y+2z-4=0$ và $\left(Q\right): 2x-y+2z+5=0$. Mặt cầu (S) tiếp xúc với hai mặt phẳng (P) và (Q) có bán kính bằng

Đồ thị hàm số y = ln x đi qua điểm 

Cho tập hợp M gồm 15 điểm phân biêt. Số vecto khác $\overrightarrow{0}$, có điểm đầu và điểm cuối là các điểm thuộc M là

Hỏi nếu tăng chiều cao của một khối trụ lên gấp 2 lần và tăng bán kính đáy của nó lên gấp 3 lần thì thể tích của khối trụ mới sẽ tăng bao nhiêu lần so với thể tích khối trụ ban đầu?

Trong không gian Oxyz, cho mặt phẳng $\left(P\right): 2x-2y+z-1=0$. Khoảng cách từ điểm M(1;-2;0) đến mặt phẳng (P) bằng

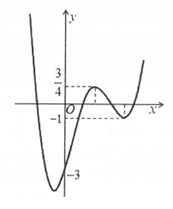
Cho hàm số bậc bốn y = f(x) có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để phương trình $f\left(\left|x+m\right|\right)=m$ có 4 nghiệm phân biệt là

Trong không gian, cho hai điểm A, B cố định và độ dài đoạn thẳng AB bằng 4. Biết rằng tập hợp các điểm  sao cho $MA=3MB$ là một mặt cầu. Bán kính của mặt cầu bằng

Gọi S là tập hợp giá trị thực của tham số m sao cho phương trình $z^2-\left(m+4\right)z+m^2+3=0$ có nghiệm phức $z_0$ thỏa mãn $\left|z_0\right|=2$. Số phần tử của tập hợp S là