Cho hàm số f(x)=$\sqrt{1+\mathrm{x}}+({\mathrm{a}}^2-2\mathrm{a}-2)\sqrt{{\mathrm{a}}^4-10{\mathrm{a}}^2+10-\mathrm{x}}$  Trong đó a là tham số. Có bao nhiêu giá trị a để f là hàm số chẵn

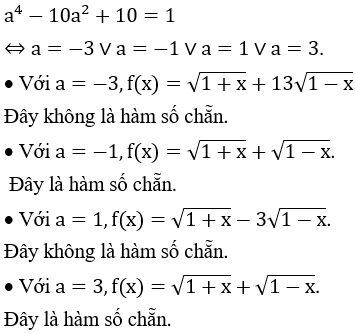
Quay hình phẳng giới hạn bởi parabol (P):${\mathrm{y}}^2=\mathrm{x}$ và đường thẳng (D): x = 1 quanh Ox, thì được một vật thể tròn xoay có thể tích là

Tính diện tích của hình giới hạn bởi đồ thị hàm số $\mathrm{y}={\mathrm{ax}}^3+{\mathrm{bx}}^2+\mathrm{cx}+\mathrm{d}$, trục hoành và hai đường thẳng x=1,x=3 (phần được tô như hình vẽ), thì ta được

Hàm số nào dưới đây là một nguyên hàm của hàm số $\mathrm{f}\left(\mathrm{x}\right)={\mathrm{xe}}^{\mathrm{x}}$

Hàm số $\mathrm{y}={\mathrm{ax}}^3+{\mathrm{bx}}^2+\mathrm{cx}+\mathrm{d}$ có bảng biến thiên

thì a+b+c+d bằng

Một hình hộp chữ nhật có độ dài ba cạnh thành một cấp số nhân, thể tích của khối hộp bằng 64${\mathrm{cm}}^3$ và tổng diện tích các mặt của hình hộp chữ nhật bằng 168 ${\mathrm{cm}}^2$. Tổng độ dài các cạnh của hình hộp chữ nhật là

Đường thẳng nào sau đây là tiếp tuyến của đồ thị hàm số $\mathrm{y}={\mathrm{x}}^3-3\mathrm{x}+2$

Cho f(x)=${\log }_2\frac{2^{\mathrm{x}}+1}{2^{\mathrm{x}}-1}$ . Giá trị của biểu thức f(f(1))+f(f(2))+...+f(f(40)) bằng

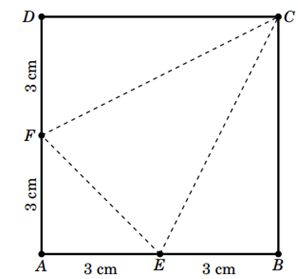
Cho hình vuông ABCD có cạnh bằng 6 cm. Gọi E, F lần lượt là trung điểm của các cạnh AB và AD. Gấp hình vuông trên để được tứ diện ACEF. Thể tích khối tứ diện ACEF là

Trong không gian Oxyz, cho tam giác OAB với O(0;0;0),A(6;0;0),B(0;8;0). Điểm M(a;b;c)thuộc mặt phẳng (P): x+2y+3z-2=0 đồng thời cách đều các đỉnh O, A, B. Giá trị của tổng a+b-c là

Cho tứ diện ABCD có BD vuông góc với AB và CD. Gọi P và Q lần lượt là trung điểm của của các cạnh CD và AB thỏa mãn BD:CD:PQ:AB = 3:4:5:6 .  Gọi $\mathrm{\phi }$ là góc giữa hai đường thẳng AB và CD. Giá trị của $\mathrm{cos\phi }$  bằng

Trong không gian Oxyz, cho tam giác ABC với A(1;2;3),B(-10;-5;-1),C(-3;-9;10). Phương trình đường phân giác kẻ từ đỉnh A của tam giác ABC là

Trong không gian Oxyz, cho mặt phẳng (P):z+2=0. Khẳng định nào sau đây sai?

Trong không gian Oxyz, cho tam giác ABC với A(-5;7;-9),B(1;3;7),C(6;-7;-3). Gọi AH là chiều cao của tam giác ABC. Tỉ số BH/CH (tỉ số giữa độ dài hai đoạn thẳng BH và CH) là

Cho số phức z thỏa z+2$\overline{\mathrm{z}}$ = 2+3i, thì |z| bằng

Cho hình cầu (S) có tâm I, bán kính bằng 13 cm. Tam giác (T) với độ dài ba cạnh là 27 cm, 29 cm, 52 cm được đặt trong không gian sao cho các cạnh của tam giác tiếp xúc với mặt cầu (S). Khoảng cách từ tâm I đến mặt phẳng chứa tam giác (T) là