Chứng minh rằng trong một tứ giác tổng độ dài hai đường chéo bao giờ cũng lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác đó.
 Giải bởi Vietjack
Giải bởi Vietjack
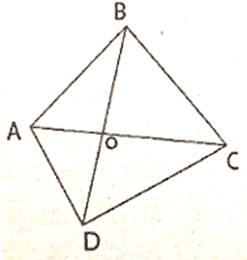
Đặt p = AB + BC + CD + DA
Ta có: OA + OD > AD (1)
OA + OB > AB (2)
OB + OC > BC (3)
OC + OD > CD (4)
Cộng vế theo vế (1), (2), (3), (4) ta có:
2(OA + OB + OC + OD) > AB + BC + CD + DA
2(AC + BD) > p
AC + BD > p/2 (*)
Mặt khác: Trong ΔABC có AC < AB + BC (5)
Trong ΔACD có AC < AD + CD (6)
Cộng vế theo vế (5) và (6) ta có:
2AC < AB + BC + CD + DA
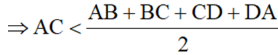
![]()
Tương tự ta cũng có BD < p/2. Suy ra: AC + BC < (p/2) + (p/2)
Hay AC + BD < p (**)
Từ (*) và (**) ta có: (p/2) < AC + BD < p.
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Trên tia đối của tia BA lấy điểm E sao cho BE = BA. Nối ED cắt AC ở I và BC ở F.
a) Chứng minh ID = 2IF.
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Trên tia đối của tia BA lấy điểm E sao cho BE = BA. Nối ED cắt AC ở I và BC ở F.
c) Biết ∠BAD = 60o, AB = a. Tính diện tích hình thoi ABCD theo a.
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Trên tia đối của tia BA lấy điểm E sao cho BE = BA. Nối ED cắt AC ở I và BC ở F.
b) Nối EO cắt BC ở G, đường thẳng OF cắt EC ở H. Chứng minh ba điểm A, G, H thẳng hàng.
Cho hình thoi ABCD. Gọi O là giao điểm hai đường chéo. Kẻ NE ⊥ PQ (E ∈ PQ), QF ⊥ MN ( F ∈ MN)
a) Chứng tỏ tứ giác NEQF là hình chữ nhật
Cho hình thoi ABCD. Gọi O là giao điểm hai đường chéo. Kẻ NE ⊥ PQ (E ∈ PQ), QF ⊥ MN ( F ∈ MN)
b) Chứng tỏ MP, NQ, EF đồng quy.
Cho hình thang ABCD (AB // CD), biết: Số đo các góc thứ tự là
Hãy điền vào chỗ (……) để được khẳng định đúng: c) Hình thoi là ………
Hãy điền vào chỗ (……) để được khẳng định đúng: b) Hình bình hành có ……… là hình chữ nhật.
Hãy điền vào chỗ (……) để được khẳng định đúng: d) Hình vuông là ………
Hãy điền vào chỗ (……) để được khẳng định đúng: a) Hình bình hành là tứ giác ………
Cho hình thang có hai đáy lần lượt là 5cm và 7cm. Độ dài đường trung bình của hình thang là: