Đề kiểm tra 45 phút Toán 8 Chương 1 Hình Học có đáp án (Đề 2)
-
8007 lượt thi
-
14 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phần trắc nghiệm (3 điểm)
Cho hình thang ABCD (AB // CD), biết: Số đo các góc thứ tự là
Xem đáp án
Chọn A
Câu 2:
Hãy điền vào chỗ (……) để được khẳng định đúng: a) Hình bình hành là tứ giác ………
Xem đáp án
a) có các cạnh đối song song
Câu 3:
Hãy điền vào chỗ (……) để được khẳng định đúng: b) Hình bình hành có ……… là hình chữ nhật.
Xem đáp án
b) một góc vuông
Câu 4:
Hãy điền vào chỗ (……) để được khẳng định đúng: c) Hình thoi là ………
Xem đáp án
c) tứ giác có bốn cạnh bằng nhau
Câu 5:
Hãy điền vào chỗ (……) để được khẳng định đúng: d) Hình vuông là ………
Xem đáp án
d) tứ giác có bốn góc vuông và bốn cạnh bằng nhau
Câu 7:
Cho hình thang có hai đáy lần lượt là 5cm và 7cm. Độ dài đường trung bình của hình thang là:
Xem đáp án
Chọn A
Câu 9:
Phần tự luận (7 điểm)
Cho hình thoi ABCD. Gọi O là giao điểm hai đường chéo. Kẻ NE ⊥ PQ (E ∈ PQ), QF ⊥ MN ( F ∈ MN)
a) Chứng tỏ tứ giác NEQF là hình chữ nhật
Xem đáp án
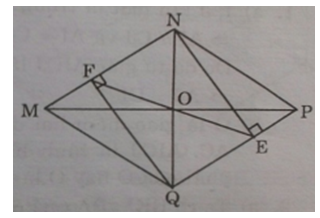
a) Ta có NF // QE (MNPQ là hình bình hành) (1)
NE ⊥ PQ; QF ⊥ MN
Mà MN // QP
⇒ NE // QF (2)
Từ (1) và (2) ⇒ tứ giác NEQF là hình bình hành có một góc vuông nên là hình chữ nhật.
Câu 10:
Cho hình thoi ABCD. Gọi O là giao điểm hai đường chéo. Kẻ NE ⊥ PQ (E ∈ PQ), QF ⊥ MN ( F ∈ MN)
b) Chứng tỏ MP, NQ, EF đồng quy.
Xem đáp án
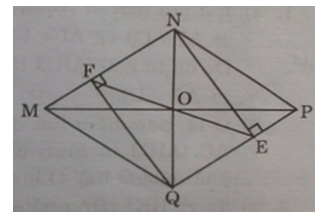
b) O là giao điểm hai đường chéo hình thoi MNPQ nên O là trung điểm NQ.
Lại có NEQF là hình chữ nhật (cmt) nên đường chéo EF phải qua trung điểm O của NQ. Vậy MP, NQ, EF đồng quy tại O.
Câu 11:
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Trên tia đối của tia BA lấy điểm E sao cho BE = BA. Nối ED cắt AC ở I và BC ở F.
a) Chứng minh ID = 2IF.
Xem đáp án
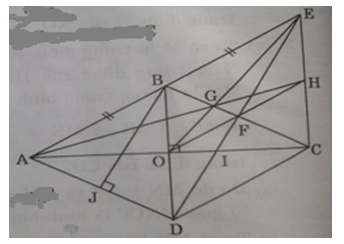
a) Ta có BE = BA (gt) mà BA // CD và BA = CD (gt)
⇒ BE // CD và BE = CD.
Do đó BECD là hình bình hành nên F là trung điểm của BC.
Xét ΔBDC có I là trọng tâm ⇒ ID = 2IF.
Câu 12:
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Trên tia đối của tia BA lấy điểm E sao cho BE = BA. Nối ED cắt AC ở I và BC ở F.
b) Nối EO cắt BC ở G, đường thẳng OF cắt EC ở H. Chứng minh ba điểm A, G, H thẳng hàng.
Xem đáp án
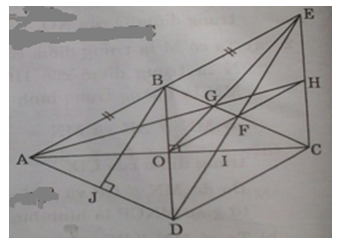
b) Xét Δ BCD có: O là trung điểm của BD
F là trung điểm của BC
⇒ OF là đường trung bình của ΔBDC ⇒ OF // DC mà DC // AB nên OF // AE
⇒ FH // BE
Mà O là trung điểm của AC nên H là trung điểm của EC hay AH là trung tuyến của ΔAEC. Mà AH cắt EO tại G nên G là trong tâm của ΔAEC ⇒ A, G, H thẳng hàng.
Câu 13:
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Trên tia đối của tia BA lấy điểm E sao cho BE = BA. Nối ED cắt AC ở I và BC ở F.
c) Biết ∠BAD = 60o, AB = a. Tính diện tích hình thoi ABCD theo a.
Xem đáp án
c) ΔABD cân (AB = AD (gt)) có ∠BAD = 60o nên ΔABD đều
kẻ BJ ⊥ AD ta có:
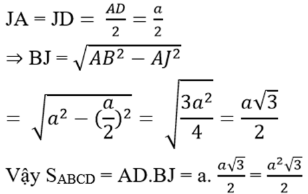
Câu 14:
Chứng minh rằng trong một tứ giác tổng độ dài hai đường chéo bao giờ cũng lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác đó.
Xem đáp án
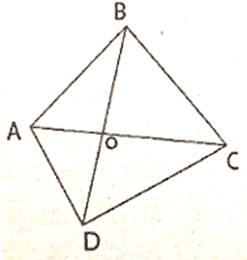
Đặt p = AB + BC + CD + DA
Ta có: OA + OD > AD (1)
OA + OB > AB (2)
OB + OC > BC (3)
OC + OD > CD (4)
Cộng vế theo vế (1), (2), (3), (4) ta có:
2(OA + OB + OC + OD) > AB + BC + CD + DA
2(AC + BD) > p
AC + BD > p/2 (*)
Mặt khác: Trong ΔABC có AC < AB + BC (5)
Trong ΔACD có AC < AD + CD (6)
Cộng vế theo vế (5) và (6) ta có:
2AC < AB + BC + CD + DA
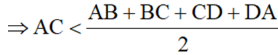
Tương tự ta cũng có BD < p/2. Suy ra: AC + BC < (p/2) + (p/2)
Hay AC + BD < p (**)
Từ (*) và (**) ta có: (p/2) < AC + BD < p.