Cho các hình thoi ABCD có cạnh AB cố định . Tìm quỹ tích giao điểm của hai đường chéo của hình thoi đó .
A. Quỹ tích điểm O là 2 cung chứa góc dựng trên AB
B. Quỹ tích điểm O là nửa đường tròn đường kính AB, trừ hai điểm A và B
C. Quỹ tích điểm O là 2 cung chứa góc dựng trên AB
D. Quỹ tích điểm O là 2 cung chứa góc dựng trên AB
Giải bởi Vietjack
Chọn đáp án B
Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường
Suy ra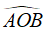 
=
Ta có 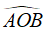= không đổi mà cố định
⇒ Quỹ tích điểm O là nửa đường tròn đường kính AB trừ hai điểm A và B
Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF.Bx của nửa kia đường tròn (O) ( với F là tiếp điểm ). Tia AF cắt tia Bx của nửa đường tròn tại D. Khi đó tứ giác OBDF là :
Cho lục giác đều ABCDEF nội tiếp đường tròn tâm O. Tính số đo góc AOB
Cho hai tiếp tuyến tại A và B cuả đường tròn (O) cắt nhau tại M , biết
Tính
Cho nửa đường tròn (O) đường kính AB. Trên tia đối AB lấy điểm M. Vẽ tiếp tuyến MC với nửa đường tròn . Gọi H là hình chiếu của C trên AB. CA là tia phân giác của góc nào dưới đây?
Góc ở hình nào dưới đây biểu diễn góc tạo bởi tiếp tuyến và dây cung
Cho tam giác ABC có BC cố định và góc A bằng . Gọi D là giao điểm của ba đường phân giác trong tam giác. Tìm quỹ tích điểm D
Cho hai tiếp tuyến tại A và B cuả đường tròn (O) cắt nhau tại M , biết
Số đo cung AB nhỏ và số đo cung AB lớn lần lượt là
Cho đường tròn (O) và điểm I nằm ngoài (O). Từ điểm I kẻ hai dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D)
Tích IA.IB bằng
