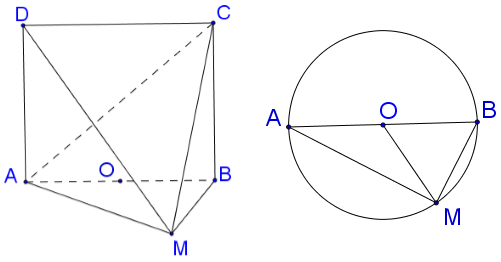
Cho hình trụ thiết diện qua trục hoành là hình vuông ABCD cạnh $4\sqrt{3}\mathrm{cm}$ với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung AB sao cho $\widehat{\mathrm{ABM}=}{60}^{\mathrm{o}}$. Tính thể tích của khối tứ diện ACDM

Cho hàm số $\mathrm{y}=\left({\mathrm{x}}^2+2\mathrm{x}-2\right){\mathrm{e}}^{\mathrm{x}}.$ Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên [0;1] bằng bao nhiêu?

Trên mặt phẳng tọa độ các điểm A,B,C lần lượt là điểm biểu diễn các số phức ${\mathrm{i}}^3,\frac{3-\mathrm{i}}{1-\mathrm{i}},\frac{\left(5+3\mathrm{i}\right)\left(1-\mathrm{i}\right)}{2}.$ Khi đó tam giác ABC.

Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình H. Hỏi H có mấy trục đối xứng?

Cho ba đường thẳng a, b, c đôi một cắt nhau và không đồng phẳng. Tìm số giao điểm phân biệt của ba đường thẳng đã cho.

Trong không gian với hệ trục tọa độ Oxyz, gọi $\left(\alpha \right)$ là mặt phẳng cắt ba trục tọa độ tại ba điểm $\mathrm{A}\left(2;0;0\right),\mathrm{B}\left(0;3;0\right),\mathrm{C}\left(0;0;1\right).$ Phương trình của $\left(\alpha \right)$ là

Cho khối chóp S.ABC có $\mathrm{SA}=\mathrm{a},\mathrm{SB}=2\mathrm{a},\mathrm{SC}=3\mathrm{a}.$ Thể tích lớn nhất của khối chóp là

Trong mặt phẳng tọa độ Oxy cho hai đường thẳng song song a và b lần lượt có phương trình $2\mathrm{x}-\mathrm{y}+4=0$ và $2\mathrm{x}-\mathrm{y}-1=0$. Tìm giá trị thực của tham số m để phép tịnh tiến T theo vectơ $\overrightarrow{\mathrm{u}}=\left(\mathrm{m};-3\right)$ biến đường thẳng a thành đường thẳng b.

Giả sử f(x) là hàm liên tục trên R và các số thực $\mathrm{a}<\mathrm{b}<\mathrm{c}$. Mệnh đề nào sau đây sai?

Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình $2\mathrm{x}+\mathrm{y}-1=0$. Để phép tịnh tiến theo vecto $\overrightarrow{v}$ biến d thành chính nó thì $\overrightarrow{v}$ là vecto nào trong các vecto sau?

Số điểm biểu diễn nghiệm của phương trình ${\cos }^2\mathrm{x}+\mathrm{sinxcosx}+\mathrm{cosx}-\mathrm{sinx}=0$ trên đường tròn lượng giác là

Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm. Tính xác suất để trong 5 sản phẩm được chọn không có phế phẩm nào.

Hàm $\mathrm{y}=-{\mathrm{x}}^3-3{\mathrm{x}}^2+2$ có giá trị cực tiểu $y_{CT}$ là

Tìm giới hạn $\underset{\mathrm{x}\to -\infty }{\lim }\frac{\sqrt{{\mathrm{x}}^2-\mathrm{x}}}{\mathrm{x}+3}$

Một ô tô đang chạy đều với vận tốc 15m/s thì phía trước xuất hiện chướng ngại vật nên người lái đạp phanh gấp. Kể từ thời điểm đó, ô tô chuyển động chậm dần đều với gia tốc $a \left(\mathrm{m}/{\mathrm{s}}^2\right).$ Biết ôtô chuyển động được thêm 30m thì dừng hẳn. Hỏi a thuộc khoảng nào dưới đây?

Hàm số $\mathrm{y}=2{\cos }^{2}2\mathrm{x}$ tuần hoàn với chu kì