Cho mặt cầu (S):(x+1)2+(y-2)2+(z-3)2=25 và mặt phẳng (α):2x+y-2z+m=0. Các giá trị của m để (α) và (S) không có điểm chung là:
A. m≤-9 hoặc m≥21
B. m<-9 hoặc m>21
C. -9≤m≤21
D. -9<m<21
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Mặt cầu (S) có tâm I(-1;2;3) và bán kính R = 5.
YCBT ⇔d(I;(α))>R⇔|-2+2-6+m|3>5⇔[m-6>15m-6<-15⇔[m>21m<-9.
Đồ thị hàm số y=√x2-4x2-5x+6 có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức G(x)=0,024x2(30-x), trong đó x là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp (x được tính bằng mg). Tìm lượng thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.
Tìm tất cả các đường tiệm cận đứng của đồ thị hàm số y=x3-3x2+20x2-5x-14.
Cho hàm số f(x)=4x4x+2.
Tính tổng S=f(12015)+f(22015)+f(32015)+...+f(20132015)+f(20142015)
Cho hai số phức z1,z2 thỏa mãn |z1|=|z2|=|z1-z2|=1. Tính giá trị của biểu thức P=(z1z2)2+(z2z1)2.
Cho một đa giác đều 20 đỉnh nội tiếp trong đường tròn O. Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Tính xác suất sao cho 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật
Cho hai số thực dương a và b. Rút gọn biểu thức A=a13√b+b13√a6√a+6√b.
Cho khối nòn đỉnh O, trục OI. Mặt phẳng trung trực của OI chia khối chóp thành hai phần. Tỉ số thể tích của hai phần là:
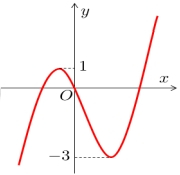
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y = |f(x)+m| có ba điểm cực trị là
Tính số cách rút ra đồng thời hai con bài từ cỗ bài tú lơ khơ 52 con.
Cho tứ diện S.ABC trên đoạn thẳng SA, SB, SC lần lượt lấy các điểm M, N, P sao cho SM = 5 MA, SN = 2NB và SP = kPC. Kí hiệu VT là thể tích của khối đa diện T. Biết rằng VSMNP=12VSABC. Tìm k?
Tìm tất cả các giá trị thực của tham số m để hàm số y=ln(x2-2mx+4) xác định với mọi x∈ℝ.
Một nguyên hàm của f(x)=(2x-1)e1x là F(x)=(ax2+bx+c+dx)e1x. Tính a+b+c+d
Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB’D’.
Tìm hệ số của x4 trong khai triển nhị thức Newton (2x+15√x)n với x > 0, biết n là số tự nhiên lớn nhất thỏa mãn A5n≤18A4n-2.