Một công ty dự kiến chi 1 tỷ đồng để sản xuất các thùng đựng sơn hình trụ có dung tích 5 lít. Biết rằng chi phí để làm mặt xung quanh của thùng đó là 100 000đ m/chi phí để làm mặt đáy là 120 000đ m/. Hãy tính số thùng sơn tối đa mà công ty đó sản xuất được (giả sử chi phí cho các mối nối không đáng kể).
A. 58135 thùng
B. 57582 thùng
C. 18209 thùng
D. 12525 thùng
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Gọi R và h lần lượt là bán kính và chiều cao của 1 thùng sơn
Suy ra dung tích 1 thùng sơn:
Gọi n là số thùng sơn tối đa sản xuất được
Tổng chi phí đó bỏ ra là:
Mà
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sinx trên đoạn lần lượt là
Cho hàm số có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y = f '(x) cho bởi hình vẽ dưới đây.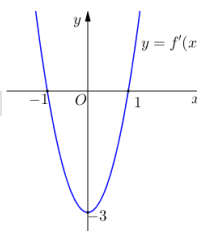 Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
Tính diện tích S của hình phẳng giới hạn bởi đồ thị (C) và trục hoành.
Một đội gồm 5 nam và 8 nữ. Lập một nhóm gồm 4 người hát tốp ca, tính xác suất để trong 4 người được chọn có ít nhất 3 nữ
Trong không gian Oxyz, mặt phẳng (P):6x - 3y + 2z - 6 = 0. Tính khoảng cách d từ điểm M(1;-2;3) đến mặt phẳng (P).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên SD = . Tính thể tích khối chóp S.ABCD theo a.
Bác An có ba tấm lưới mắt cáo, mỗi tấm có chiều dài 4 m. Bác muốn rào một phần vườn của nhà bác dọc theo bờ tường (bờ tường ngăn đất nhà bác với đất nhà hàng xóm) theo hình thang cân ABCD (như hình vẽ) để trồng rau (AB là phần tường không cần phải rào). Bác An rào được phần đất vườn có diện tích lớn nhất gần với giá trị nào nhất sau đây?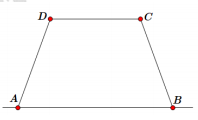
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD. DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?
Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số (x;y) thỏa mãn đồng thời thỏa mãn .
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc nhau và SA = SB = SC = a. Tính thể tích của khối chóp S.ABC.
Cho mặt cầu (S) bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất
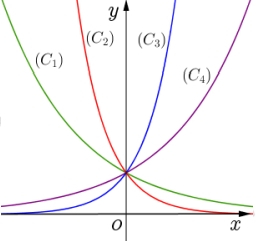
Cho bốn hàm số , , có đồ thị là 4 đường cong theo phía trên đồ thị, thứ tự từ trái qua phải là như hình vẽ. Tương ứng hàm số - đồ thị đúng là