Với giá trị lớn nhất của a bằng bao nhiêu để phương trình có nghiệm?
A. 2
B.
C. 4
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Ta có
Phương trình (*) có nghiệm khi và chỉ khi .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SBC) và (ABCD) bằng . Tính tỉ số biết V là thể tích của khối chóp S.ABCD?
Cho y = f(x) là hàm số chẵn, liên tục trên biết đồ thị hàm số y = f(x) đi qua điểm
và , tính
Tập nghiệm của bất phương trình có dạng S = [a;b]. Giá trị b - 2a thuộc khoảng nào sau đây?
Cho hình lập phương ABCD. A’B’C’D’ có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A’B’C’D’. Kết quả tính diện tích toàn phần của hình nón đó có dạng bằng với b, c là hai số nguyên dương và b > 1. Tính giá trị của bc?
Cho hàm số y = f(x) liên tục trên và có đồ thị như hình dưới. Biết rằng trục hoành là tiệm cận ngang của đồ thị. Tìm tất cả các giá trị thực của tham số m để phương trình có hai nghiệm phân biệt dương.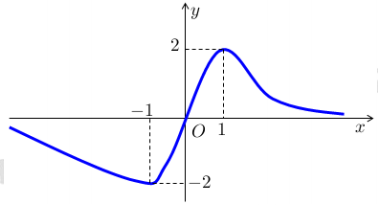
Cho ab, là các số thực dương thỏa mãn . Hỏi giá trị nhỏ nhất của biểu thức sau là:
Xét tứ diện OABC có OA, OB, OC đôi một vuông góc nhau. Gọi lần lượt là góc giữa các đường thẳng OA, OB, OC với mặt phẳng (ABC). Khi đó giá trị nhỏ nhất của biểu thức 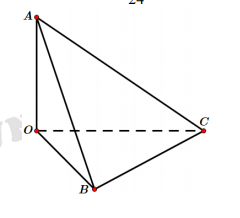
Biết rằng khi quay một đường tròn có bán kính bằng 1 quanh đường kính của nó thì ta được một mặt cầu. Tính diện tích mặt cầu đó.
Một hộp đựng 9 viên bi trong đó có 4 viên bi đỏ và 5 viên bi xanh. Lấy ngẫu nhiên từ hộp 3 viên bi. Tìm xác suất để 3 viên bi lấy ra có ít nhất 2 viên bi màu xanh.
Biết luôn có hai số a và b để là nguyên hàm của hàm số f(x) thỏa mãn . Khẳng định nào sau đây đúng và đầy đủ nhất?
Cho n là số nguyên dương thỏa mãn . Hệ số của số hạng chứa của khai triển biểu thức bằng:
Một vật chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc tính theo thời gian t là . Tính quãng đường vật đi được trong khoảng 10s kể từ khi bắt đầu tăng tốc.