Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Khẳng định nào sau đây là đúng nhất.
A. OA + OB + OC + ODAB + BC + CD + DA.
B. .
C. Cả A và B đều đúng.
D. Cả A và B đều sai.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án cần chọn là:C
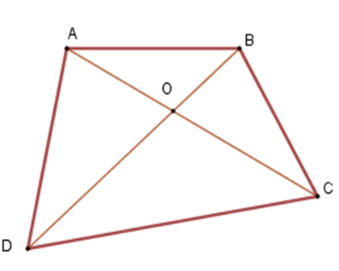
+ Xét tam giác OAB ta có OA + OB AB (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại).
Tương tự ta có OC + OD CD; OB + OC BC; OA + OD AD
Cộng vế với vế ta được
OA + OB + OC + OD + OB + OC + OA + OD AB + BC + CD + AD
2(OA + OB + OC + OD) AB + BC + CD + DA
OA + OB + OC + OD nên B đúng
+ Xét tam giác ABC có AB + BC AC (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại).
Tương tự ta có BC + CD BD; CD + DA AC; AD + DB BD
Cộng vế với vế ta được
AB + BC + BC + CD + CD + DA + DA + AB AC + BD + AC + BD
2(AB + BC + CD + DA) 2(AC + BD)
AB + BC + CD + DA AC + BD mà AC + BD = OA + OC + OB + OD nên
OA + OB + OC + OD AB + BC + CD + DA nên A đúng
Vậy cả A, B đều đúng.
Tứ giác ABCD có . Các tia phân giác của các góc B và D cắt nhau tại I. Tính số đô góc BID.
Cho tứ giác ABCD biết số đo của các góc tỉ lệ thuận với 4; 3; 5; 6. Khi đó số đo các góc lần lượt là:
Cho tứ giác ABCD biết số đo của các góc tỉ lệ thuận với 4; 9; 7; 6. Khi đó số đo các góc lần lượt là :
Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D = 4:3:2:1. Số đo các góc theo thứ tự đó là ?
Tam giác ABC có các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc .