Chia tấm bìa hình tròn bán kính cm thành 3 phần (như hình vẽ). lấy một phần và uốn thành một hình nón có đường sinh là bán kính của hình tròn trên. Khi đó thể tích của khối nón tạo thành là:
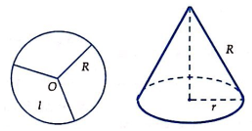
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A.
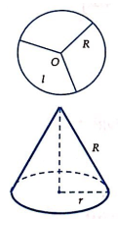
Gọi hình nón tạo thành có bán kính là r
Chu vi đáy là
![]()
chu vi của hình tròn đầu)
=> r = R/3
Hình nón có đường sinh là R => Chiều cao
![]()
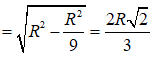
Thể tích khối nón tạo thành là
![]()
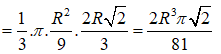
Cho hình trụ có bán kính đáy bằng a, chu vi của thiết diện qua trục bằng 12a. Thể tích của khối trụ đã cho bằng
Trong các khối trụ có thể tích V không đổi thì hình trụ có diện tích toàn phần lớn nhất khi tỉ lệ giữa chiều cac h và bán kính đáy R là:
Xét các mệnh đề sau:
(I) Có một và chỉ một đường thẳng đi qua 2 điểm phân biệt.
(II) Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt.
(III) Nếu 2 mặt phẳng có một điểm chung thì chúng có duy nhất một điểm chung khác nữa.
(IV) Nếu 1 đường thẳng có 2 điểm phân biệt thuộc mặt phẳng thì mọi điểm của đường thẳng đó đều thuộc mặt phẳng.
Số mệnh đề sai là:
Khối đa diện nào sau đây có các mặt không phải là tam giác đều?
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm BC và BD. Khi đó gọi là thể tích cảu ABCD và là thể tích của ABMN thì tỉ số là:
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M,N lần lượt là trung điểm của BB', CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai phần, là thể tích của phần đa diện chứa điểm B, thể tích phần đa diện còn lại. Tính tỉ số
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng . Gọi lần lượt thể tích khối cầu và khối nón ngoại tiếp hình chóp S.ABCD. Tính tỷ số
Cho hình lăng trụ ABC.A’B’C’ độ dài cạnh bên là 2a, dáy ABC là tam giác vuông tại A, AB = a, AC = . Hình chiếu của A’ lên (ABC) trùng với trung điểm I của BC. Khi đó cos(AA';B'C') là:
Cho tứ diện ABCD có AB = 3a, AC = 5a, AD = 4a, các góc . Khi đó thể tích khối ABCD là:
Hình chóp đều S.ABCD. Gọi O là giao điểm của AC và BD. Phát biểu nào dưới đây là đúng?
Cho hình nón tròn xoay có đường cao h = 40 (cm), bán kính đáy r = 50 (cm). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 24 (cm). Tính diện tích của thiết diện
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng . Tính tỉ số thể tích của hình trụ (T) và hình nón (T) .
Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều, độ dài cạnh AB = 2a. Hình chiếu vuông góc của A' lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng , tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACC'A')
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N). lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai