Cho hình lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng , cạnh AB = a. Thể tích V của khối lăng trụ đó là:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
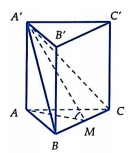
Gọi M là trung điểm BC. Ta có
AM là trung tuyến trong tam giác đều cạnh a nên AM =
![]()
![]()
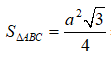
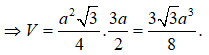
Giá trị lớn nhất của thể tích khối nón nội tiếp trong khối cầu có bán kính R là:
Cho khối trụ (T), AB và CD lần lượt là hai đường kính trên hai mặt đáy của (T). Biết góc giữa AB và CD là 30°, AB = 6 và thể tích khối ABCD là 30. Khi đó thể tích khối trụ (T) là:
Khối trụ tròn xoay có đường cao với bán kính đáy bằng a thì thể tích bằng:
Cho các mệnh đề sau:
(I) 3 vecto gọi là đồng phẳng khi và chỉ khi chúng cùng nằm trong một mặt phẳng.
(II) 3 vecto gọi là đồng phẳng khi và chỉ khi chúng có giá song song với một mặt phẳng.
(III) 3 vecto đồng phẳng nếu tồn tại duy nhất bộ số (m,n) sao cho .
Số mệnh đề đúng là:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân đỉnh A, , BC' tạo với (ABC) góc . Gọi I là trung điểm AA', biết . Tính
Cho tam giác đều ABC cạnh 1 và hình vuông MNPQ nội tiếp trong tam giác ABC(MAB, NAC, P,QBC) . Gọi S là phần mặt phẳng chứa các điểm thuộc tam giác ABC nhưng không chứa các điểm thuộc hình vuông MNPQ. Thể tích của vật thể tròn xoay khi quay S quanh trục là đường thẳng qua A vuông góc với BC là:
Cho hình trụ có khoảng cách giữa hai đáy bằng 10. Biết diện tích xung quanh của hình trụ bằng , thể tích của khối trụ là:
Cho hình chóp S.ABCD có đáy là hình thang (AD//BC). Gọi M là trọng tâm của SAD, N là điểm thuộc đoạn AC sao cho NA = NC. P là điểm thuộc đoạn CD sao cho PD =PC. Khi đó mệnh đề nào sau đây đúng?
Một hình hộp chữ nhật có độ dài ba cạnh cùng xuất phát từ một đỉnh lần lượt là 2, 3, 4. Khi đó thể tích của hình hộp chữ nhật đó là:
Cho lăng trụ ABC.A’B’C’. Gọi M là trung điểm của A’B’. Điểm N thay đổi trên đoạn BB’. Gọi P là trung điểm của C'N, B'P CC' = Q. Khi đó MP luôn thuộc mặt phẳng cố định thỏa mãn:
Cho tam giác ABC vuông cân tại B, cạnh AB = 2. Quay đường gấp khúc ACB quanh cạnh AB ta được hình nón. Tính diện tích xung quang của hình nón đó.
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân đỉnh A, , BC' tạo với (ABC) góc . Gọi I là trung điểm AA', biết . Tính
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng 2a. Một hình trụ có hai đáy là hai hình tròn nội tiếp trong hai hình vuông ABCD và A’B’C’D’. Tính thể tích của khối lăng trụ tạo nên từ hình trụ trên.