Cho bất phương trình Giá trị thực của tham số để bất phương trình trên có nghiệm duy nhất thuộc khoảng nào sau đây?
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đặt khi đó bất phương trình đã cho trở thành
Điều kiện của bất phương trình là Ta có:
Đặt
* Với Ta có
Vì là hàm tăng trên nên từ ta có
vô số nghiệm vì với Suy ra không thỏa bài toán.
* Với Ta có
Xét , ta có
+ thì vô nghiệm. Không thỏa bài toán.
+ thì có nghiệm là đoạn , lúc này nhận hơn 1 số của làm nghiệm. Không thỏa bài toán.
+ thì có nghiệm duy nhất và thỏa Do đó bất phương trình có nghiệm duy nhất là
Vậy
Chọn đáp án C.
Một tổ học sinh có 5 học sinh nam và 7 học sinh nữ. Có bao nhiêu cách chọn 4 học sinh của tổ đó tham gia đội xung kích?
Một nhóm gồm 10 học sinh trong đó có An và Bình, đứng ngẫu nhiên thành một hàng. Xác suất để An và Bình đứng cạnh nhau là
Cho hình lăng trụ đứng có đáy là tam giác vuông tại Đường chéo của mặt bên tạo với mặt phẳng một góc bằng . Tính thể tích khối lăng trụ theo
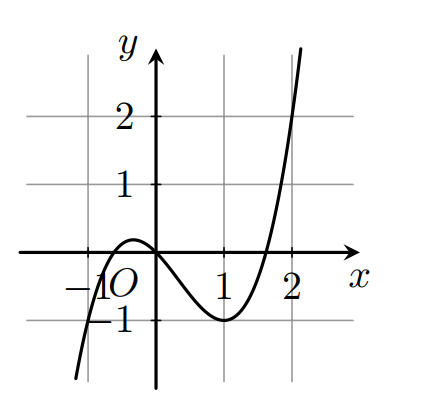
Cho hàm số có đạo hàm trên Biết rằng hàm số có đồ thị như hình bên. Đặt Hỏi hàm số có bao nhiêu điểm cực đại và bao nhiêu điểm cực tiểu?
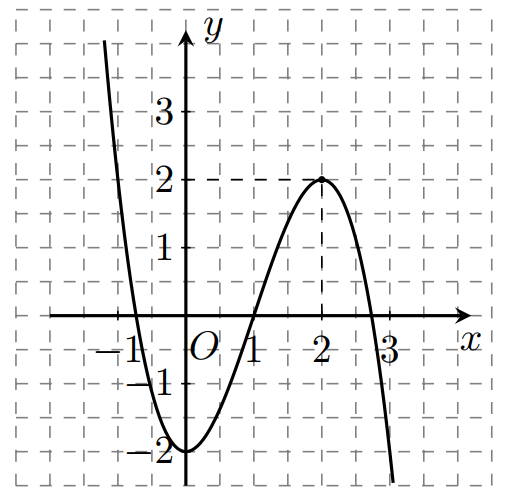
Cho hàm số liên tục trên Biết rằng đồ thị của hàm số được cho bởi hình vẽ bên. Vậy khi đó hàm số có bao nhiêu điểm cực đại?
Trong không gian tọa độ xác định phương trình mặt cầu có tâm và tiếp xúc mặt phẳng
Trong không gian mặt phẳng đi qua điểm và nhận làm một véc tơ pháp tuyến có phương trình là
Hình chóp có đáy là tam giác vuông tại với và với là trung điểm Biết khoảng cách giữa hai đường thẳng và bằng Tính cos góc giữa hai mặt phẳng và .
Trong không gian một véc-tơ chỉ phương của đường thẳng chứa trục có tọa độ là