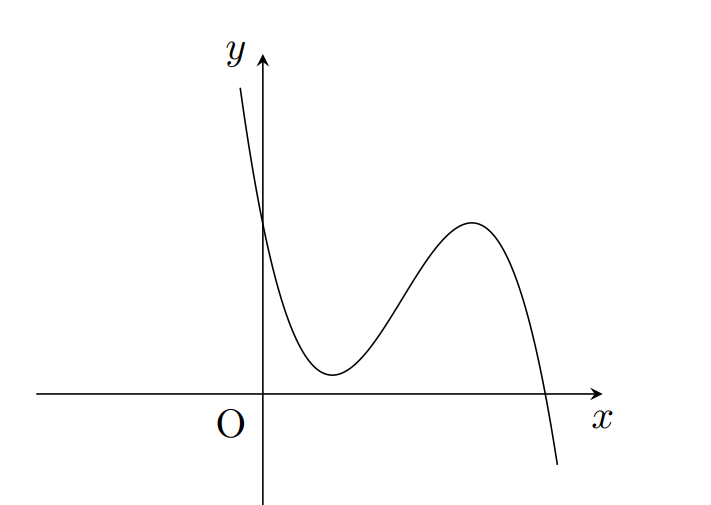
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
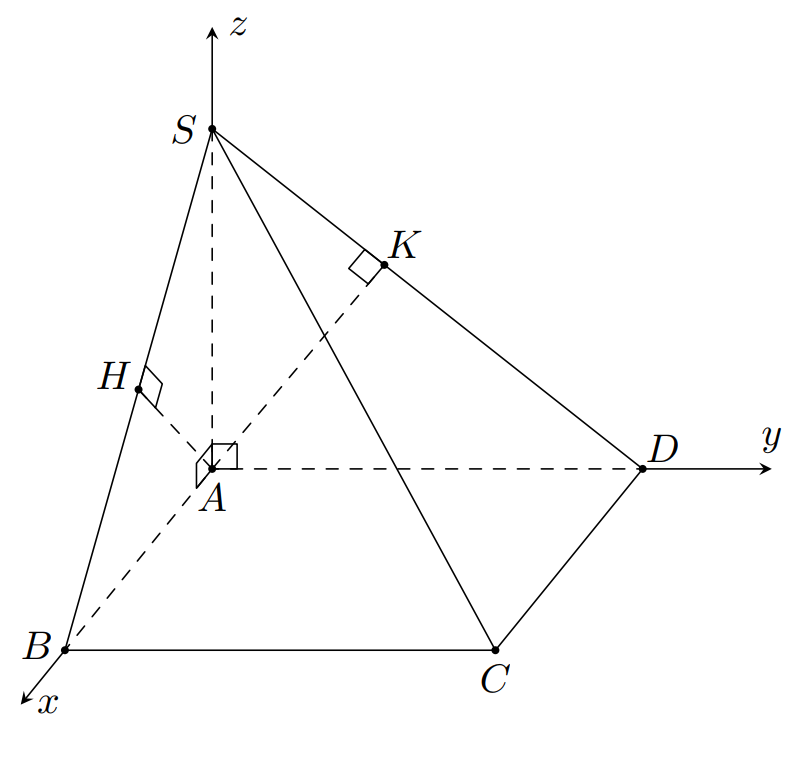
Đặt với
Trong mặt phẳng kẻ tại trong mặt phẳng , kẻ tại
Dễ dàng chứng minh được , và là trung điểm của
Chọn hệ trục tọa độ như hình vẽ
Ta có:
Suy ra:
Trong tam giác vuông tại có
.
Do lần lượt là hai véc-tơ pháp tuyến của hai mặt phẳng và nên
Thể tích khối chóp là
Chọn đáp án B.
Cho hàm số xác định, liên tục trên và có bảng biến thiên sau
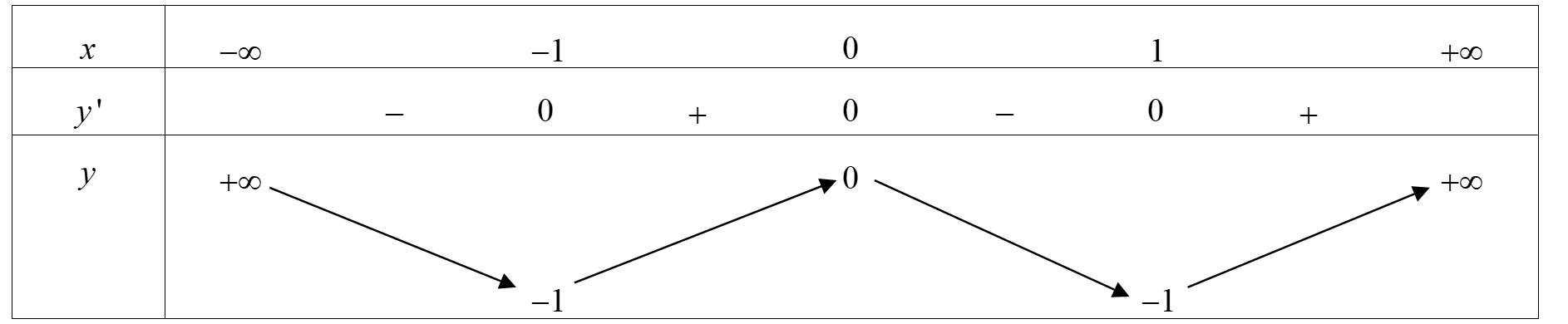
Cho hàm số liên tục trên bảng biến thiên của hàm số như sau:
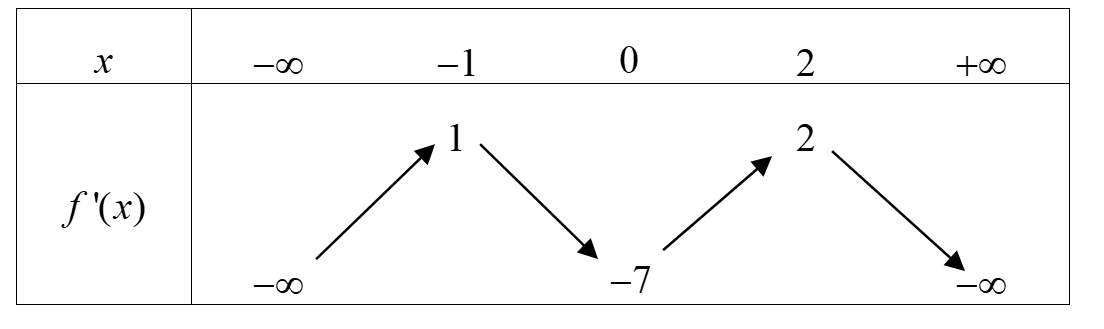
Số điểm cực trị của hàm số là
Trong không gian với hệ tọa độ cho mặt phẳng và điểm . Viết phương trình mặt cầu có tâm và cắt mặt phẳng theo giao tuyến là đường tròn có bán kính bằng 5.
Tập hợp tất cả các số thực không thỏa mãn bất phương trình là khoảng Tính
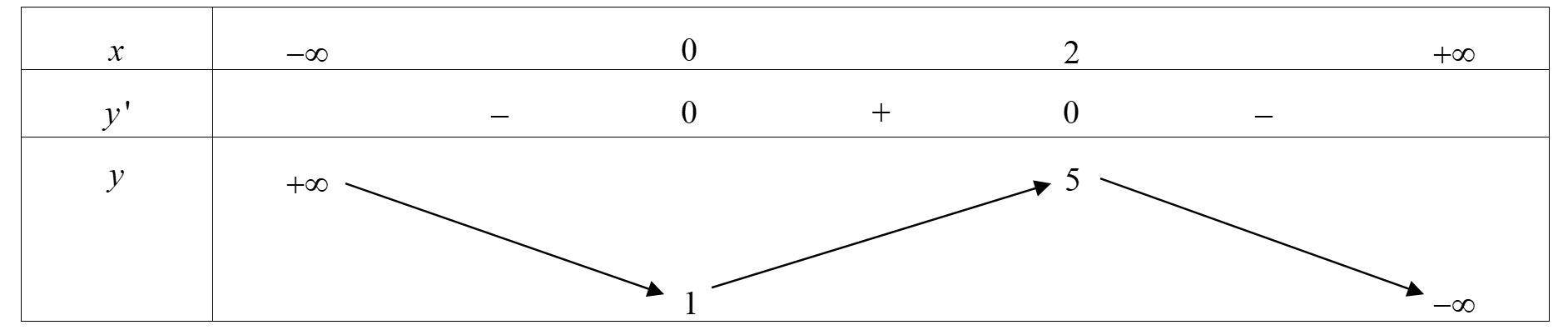
Cho hàm số có bảng biến thiên như hình vẽ. Hàm số đạt cực đại tại điểm
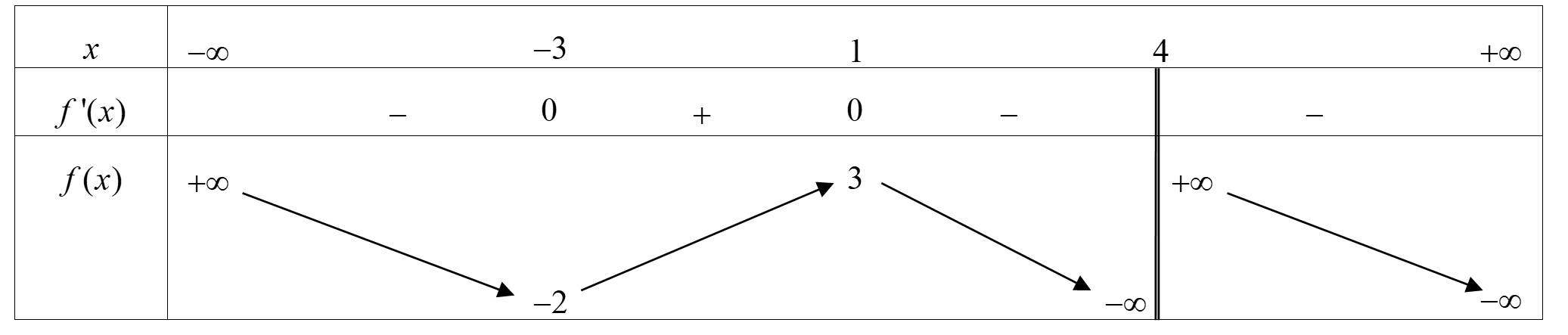
Cho hàm số có bảng biến thiên như hình bên. Mệnh đề nào sau đây là đúng?
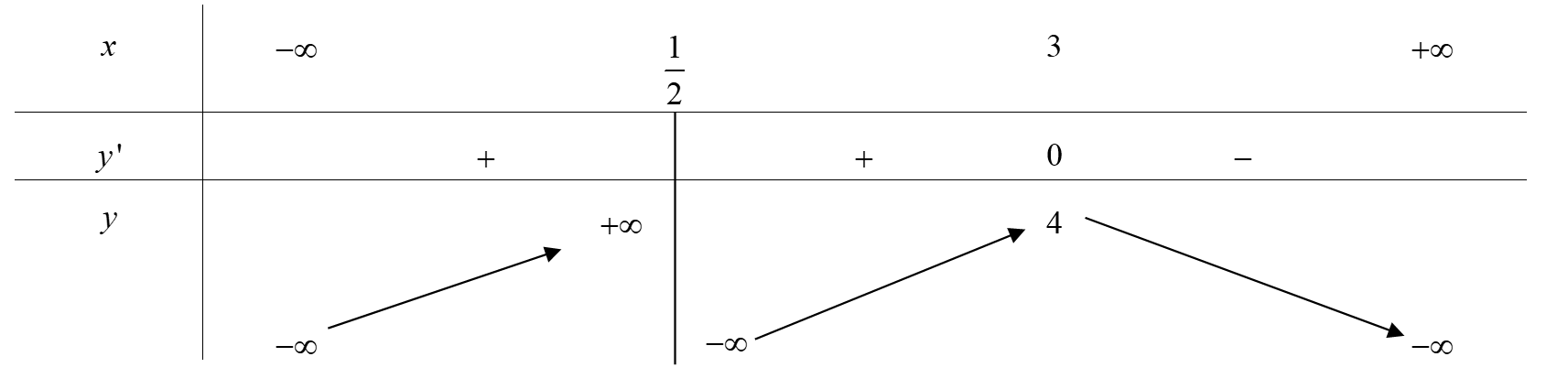
Trong không gian với hệ tọa độ cho đường thẳng Phương trình nào dưới đây là phương trình chính tắc của đường thẳng
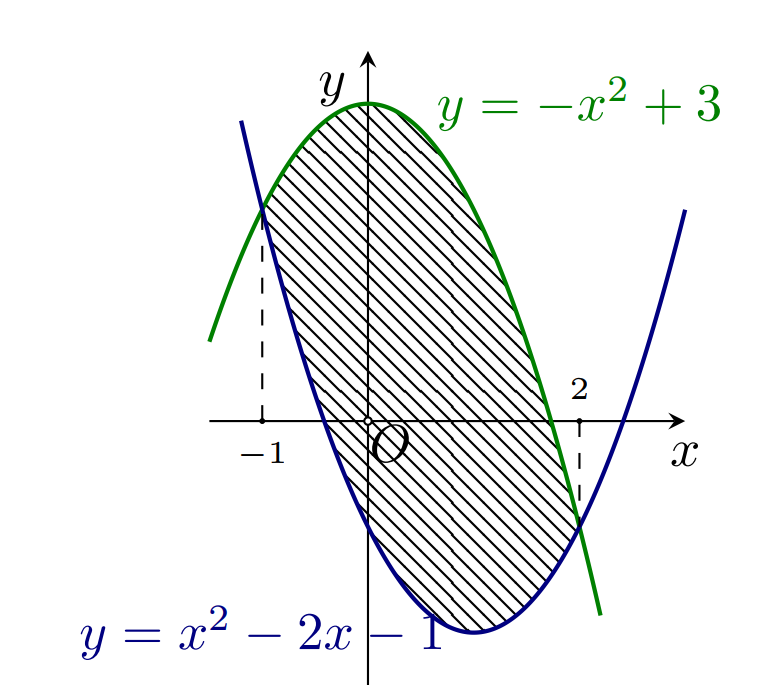
Cho hàm số . Hàm số có đồ thị như hình bên. Tìm số điểm cực trị của hàm số