Tìm số giá trị nguyên thuộc đoạn của tham số để đồ thị hàm số có đúng hai đường tiệm cận.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D
Xét hàm số
+) TXĐ:
+) Do đó ĐTHS có tiệm cận ngang
+) Để ĐTHS có đường tiệm cận thì phải có thêm tiệm cận đứng. Vậy yêu cầu bài toán trở thành: Tìm điều kiện để phương trình phải có nghiệm lớn hơn hoặc bằng
Trường hợp : Phương trình phải có 2 nghiệm thỏa mãn
Trường hợp : Phương trình có nghiệm thì
Với phương trình trở thành: ( tmđk)
Trường hợp : Phương trình có nghiệm kép
Khi thì phương trình có nghiệm (không thỏa mãn)
Theo đề bài , nguyên do đó
Vậy có giá trị của .
Ý kiến phản biện:
Có thể nhận xét phương trình nếu có nghiệm thì do đó luôn có ít nhất một nghiệm âm. Vậy đk bài toán chỉ thỏa mãn khi và chỉ khi có 2 nghiệm thỏa mãn
Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng và biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là một hình chữ nhật có hai kích thước là
Cho hàm số có bảng biến thiên như hình bên.
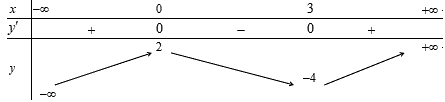
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Cho hai số thực thay đổi thỏa mãn .Giá trị lớn nhất của biểu thức là với là các số nguyên dương và tối giản. Tính .
Cho không gian , cho điểm và hai đường thẳng , . Viết phương trình mặt phẳng đi qua và song song với hai đường thẳng .
Trong không gian cho mặt phẳng và đường thẳng . Mệnh đề nào sau đây đúng ?
Cho hàm số có đồ thị như hình dưới đây
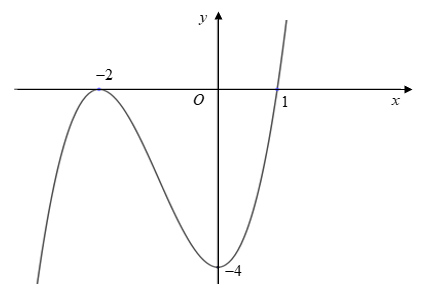
Có tất cả bao nhiêu giá trị nguyên của tham số để phương trình có nghiệm phân biệt
Cho các số thực thỏa mãn . Tính khi biểu thức đạt giá trị lớn nhất.
Cho hàm số liên tục trên R và có đồ thị như hình vẽ bên. Biết rằng diện tích các hình phẳng (A), (B) lần lượt bằng 3 và 7. Tích phân bằng
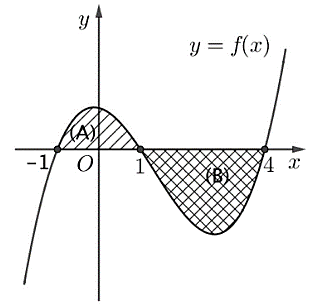
Cho hàm số bậc bốn có đồ thị như hình dưới đây. Số nghiệm của phương trình là