Biết rằng giá trị lớn nhất của hàm số \(y = \frac{{\cos x + m}}{{2 - \cos x}}\) trên đoạn \(\left[ { - \frac{\pi }{3};\frac{\pi }{2}} \right]\) bằng 1. Mệnh đề nào sau đây đúng?
A.\(\left| m \right| >2.\)
B.\(\left| m \right| = 1.\)
C.\(1 < \left| m \right| \le 2.\)
D. \(\left| m \right| < 1.\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D.
Đặt \(t = \cos x,x \in \left[ { - \frac{\pi }{3};\frac{\pi }{2}} \right] \Rightarrow t \in \left[ {0;1} \right].\)
Xét hàm số \(y = \frac{{t + m}}{{2 - t}}\) trên đoạn \(\left[ {0;1} \right]\)
Ta có: \(y' = \frac{{2 + m}}{{{{\left( {2 - t} \right)}^2}}}.\)
Nếu \(2 + m >0 \Leftrightarrow m >- 2\) thì \(y' >0,\) hàm số đồng biến trên \(\left[ {0;1} \right],\) suy ra:
\(\mathop {\max }\limits_{\left[ {0;\frac{1}{2}} \right]} f\left( t \right) = f\left( 1 \right) \Leftrightarrow f\left( 1 \right) = 1 \Leftrightarrow \frac{{1 + m}}{1} = 1 \Leftrightarrow m = 0.\)
Nếu \(2 + m < 0 \Leftrightarrow m < - 2\) thì \(y' < 0,\) hàm số nghịch biến trên \(\left[ {0;1} \right],\) suy ra:
\(\mathop {\max }\limits_{\left[ {0;\frac{1}{2}} \right]} f\left( t \right) = f\left( 0 \right) \Leftrightarrow f\left( 0 \right) = 1 \Leftrightarrow \frac{m}{2} = 1 \Leftrightarrow m = 2\) (không thỏa mãn).
Vậy \(m = 0 \Rightarrow \left| m \right| < 1.\)
Cho hai hàm số \(y = {2^x}\) và \(y = {\log _2}x\) lần lượt có đồ thị \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right).\) Gọi \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\) là hai điểm lần lượt thuộc \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) sao cho tam giác \(IAB\) vuông cân tại \(I,\) trong đó \(I\left( { - 1; - 1} \right).\) Giá trị của \(P = \frac{{{x_A} + {y_A}}}{{{x_B} + {y_B}}}\) bằng
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
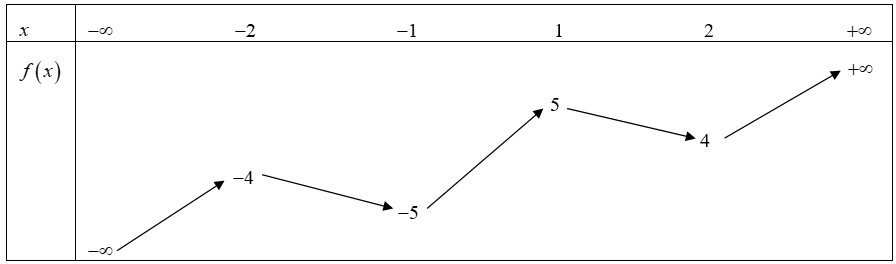
Có bao nhiêu giá trị nguyên của tham số \(m\) để trên đoạn \(\left[ { - 1;2} \right]\) phương trình \(3f\left( {{x^2} - 2x - 1} \right) = m\) có đúng hai nghiệm thực phân biệt?
Trong các hàm số dưới đây, hàm số nào nghịch biến trên khoảng \(\mathbb{R}?\)
Cho phương trình \(\log _2^2x + 2m{\log _2}x + 2m - 2 = 0\) với \(m\) là tham số. Có bao nhiêu giá trị nguyên của \(m\) để phương trình đã cho có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \({x_1} \le 64{x_2} \le 4096{x_1}?\)
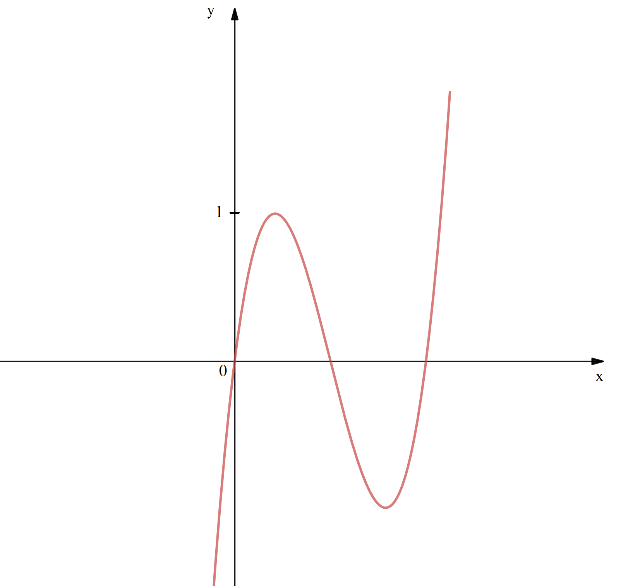
Cho hàm số \[f(x)\] có \[f(0) = 0\]. Biết rằng \[y = f'(x)\] là hàm số bậc ba và có đồ thị là đường cong trong hình dưới đây, hàm số \[g(x) = f(f(x) - x)\] có bao nhiêu điểm cực trị ?
Cho hàm số \[f(x)\] có bảng biến thiên như sau:
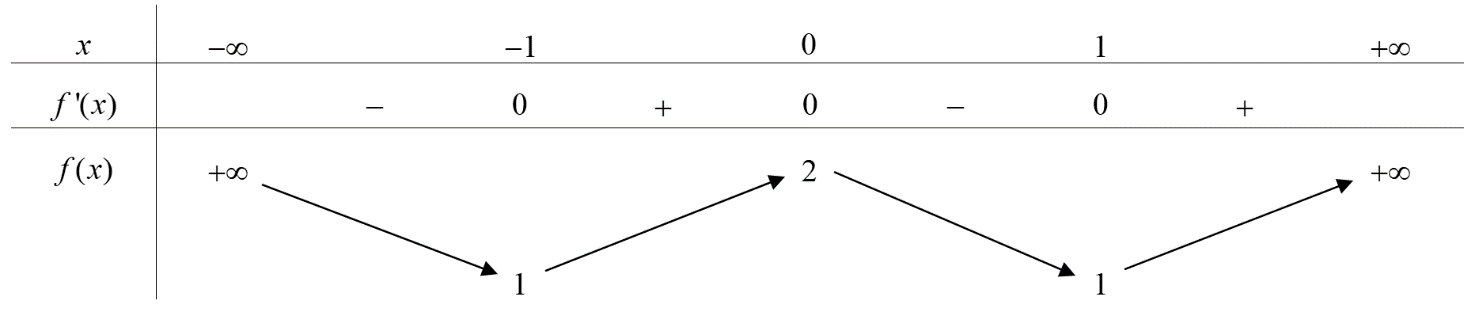
Giá trị cực tiểu của hàm số đã cho bằng
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của \(f'\left( x \right)\) như sau:

Hàm số \(y = f\left( {1 - x} \right)\) đồng biến trên khoảng nào dưới đây?
Chọn ngẫu nhiên 8 học sinh từ một nhóm học sinh có 7 học sinh nam và 5 học sinh nữ để xếp thành một hàng ngang, xác suất để hàng đó có 5 học sinh nam và 3 học sinh nữ bằng
Giá trị nhỏ nhất của hàm số \(f\left( x \right) = {x^3} - 36x\) trên đoạn \(\left[ {2;20} \right]\) bằng