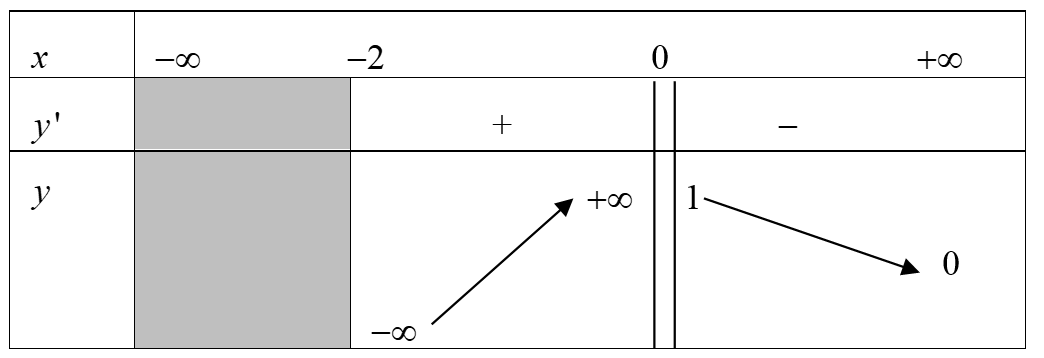
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ. Hỏi hàm số đã cho có bao nhiêu đường tiệm cận?
A. 3.
B. 2.
C. 4.
D. 1.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A.
Ta có \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 0\) nên \(y = 0\) là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right) = - \infty ,\mathop {\lim }\limits_{x \to {{\left( 0 \right)}^ + }} f\left( x \right) = + \infty \) nên \(x = - 2,x = 0\) là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Thiết diện qua trục của một hình nón là tam giác đều cạnh \(2a.\) Đường cao của hình nón là
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như hình vẽ
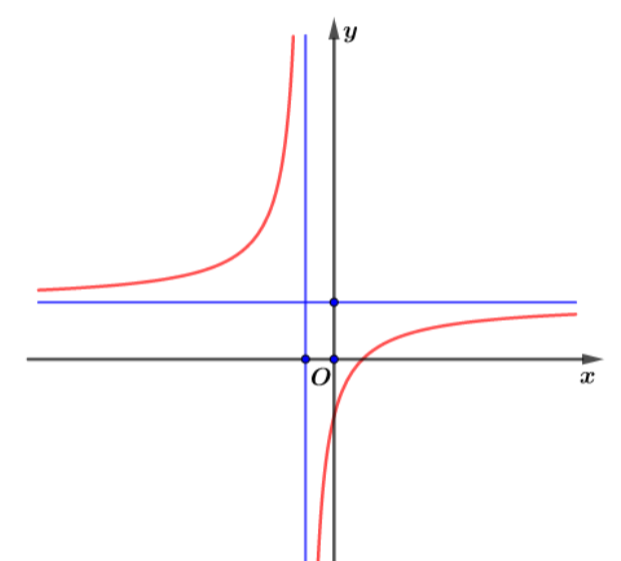
Khẳng định nào sau đây đúng?
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác với \(AB = a,AC = 2a\) và \(\widehat {BAC} = {120^0},AA' = 2a\sqrt 5 .\) Thể tích \(V\) của khối lăng trụ đã cho là
Một đề thi trắc nghiệm gồm 50 câu, mỗi câu có 4 phương án trả lời trong đó chỉ có 1 phương án đúng, mỗi câu trả lời đúng được 0,2 điểm. Một thí sinh làm bài bằng cách chọn ngẫu nhiên 1 trong 4 phương án ở mỗi câu. Tính xác suất để thí sinh đó được 6 điểm.
Xét các số thực dương \(a\) và \(b\) thỏa mãn \({\log _5}\left( {{5^a}{{.25}^b}} \right) = {5^{{{\log }_5}a + {{\log }_5}b + 1}}.\) Mệnh đề nào dưới đây đúng?
Khối chóp tứ giác \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(6a,\) tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy có thể tích bằng
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) sao cho giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{34}}{{\sqrt {{{\left( {{x^3} - 3x + 2m} \right)}^2}} + 1}}\) trên đoạn \(\left[ {0;3} \right]\) bằng 2. Tổng tất cả các phần tử của \(S\) bằng
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác vuông và \(AB = BC = a,AA' = a\sqrt 2 ,M\) là trung điểm \(BC.\) Tính khoảng cách \(d\) của hai đường thẳng \(AM\) và \(B'C.\)
Cho hình nón có góc ở đỉnh bằng \({60^0},\) bán kính đáy bằng \(a.\) Diện tích xung quanh của hình nón bằng
Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = 3{\cos ^4}x + \frac{3}{2}{\sin ^2}x + m\cos x - \frac{5}{2}\) đồng biến trên \(\left( {\frac{3}{2};\frac{{2\pi }}{3}} \right].\)
Trong khai triển \[{(a + b)^n}\], số hạng tổng quát của khai triển là.
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy là tam giác vuông cân tại \(A.\) Hình chiếu vuông góc của điểm \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm tam giác \(\left( {ABC} \right).\) Biết khoảng cách giữa hai đường thẳng \(AA'\) và \(BC\) bằng \(\frac{{\sqrt {17} }}{6}a,\) cạnh bên \(AA'\) bằng \(2a.\) Tính theo \(a\) thể tích \(V\) của khối lăng trụ \(ABC.A'B'C'\) biết \(AB < a\sqrt 3 .\)
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}.\) Biết rằng hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ
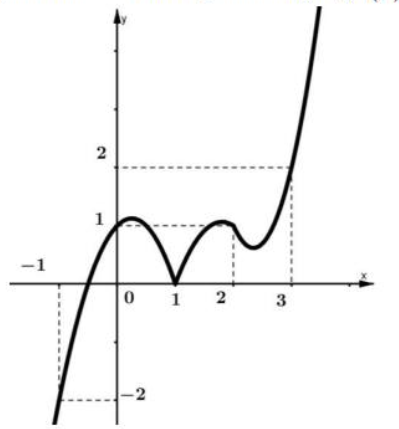
Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^2} - 2x} \right) - \left( {\frac{{{x^4}}}{2} - 2{x^3} + {x^2} + 2x + 1} \right)\) là
Rút gọn biểu thức \(P = {x^{\frac{1}{3}}}.\sqrt[6]{x}\) với \(x >0\) ta được