Cho hình vuông ABCD có các đỉnh A, B, C tương ứng nằm trên đồ thị của các hàm số và Biết rằng diện tích hình vuông bằng 36, cạnh AB song song với trục hoành. Khi đó a bằng:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Gọi
- Tính sử dụng điều kiện cạnh AB song song với trục hoành tìm m theo n.
- Tính AB giải phương trình tìm m, n.
- Tính sử dụng điều kiện tìm p.
- Giải phương trình độ dài cạnh BC tìm a
Cách giải:
Gọi
Vì ABCD là hình vuông nên .
Ta có
Vì và cùng phương nên
.
Lại có
Tương tự ta có cùng phương với nên
Mà .
Chọn B.
Chọn ngẫu nhiên hai số khác nhau từ 21 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tích là một số lẻ bằng:
Xét tất cả các số thực dương a và b thỏa mãn Mệnh đề nào dưới đây đúng?
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ sau:
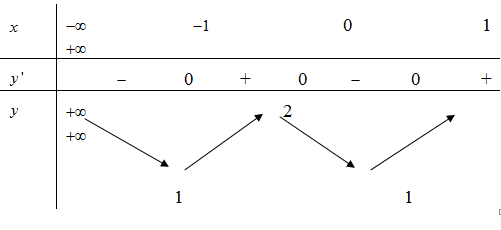
Số nghiệm thực của phương trình là:
Có bao nhiêu số nguyên a thuộc đoạn [-20; 20] sao cho hàm số có cực đại?
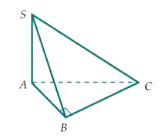
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = a, tam giác vuông tại và BC = a (minh họa hình vẽ bên dưới). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
Cho hàm số y = f(x) có đồ thị như hình vẽ sau:
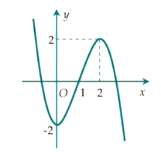
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
Trên giá sách có 8 quyển sách Văn và 10 quyển sách Toán, các quyển này đôi một phân biệt. Hỏi có bao nhiêu cách chọn ra 1 quyển sách trên giá?
Có bao nhiêu giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng