Cho hàm số\(y = {x^3} + (m - 1){x^2} - 3mx + 2m + 1\) có đồ thị , biết rằng đồ thị\(({C_m})\) luôn đi qua hai điểm cố định\(A,\,B.\) Có bao nhiêu số nguyên dương \(m\)thuộc đoạn \(\left[ { - 2020;2020} \right]\) để \(({C_m})\) có tiếp tuyến vuông góc với đường thẳng \(AB\)?
A.4041.
B. 2021.
C. 2019.
D. 2020.
 Giải bởi Vietjack
Giải bởi Vietjack
Hàm số được viết lại thành \(\left( {{x^2} - 3x + 2} \right)m + {x^3} - {x^2} + 1 - y = 0.\)
Một điểm \(M\left( {{x_0};{y_0}} \right)\) là điểm cố định của đồ thị hàm số thì phương trình \(\left( {x_0^2 - 3x_0^{} + 2} \right)m + x_0^3 - x_0^2 + 1 - {y_0} = 0\) phải nghiệm đúng với mọi \(m,\) xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}x_0^2 - 3{x_0} + 2 = 0\\x_0^3 - x_0^2 + 1 - {y_0} = 0\end{array} \right. \Rightarrow \left[ \begin{array}{l}{x_0} = 1;{y_0} = 1\\{x_0} = 2;{y_0} = 5\end{array} \right..\)
Giả sử \(A\left( {1;1} \right),B\left( {2;5} \right) \Rightarrow \overrightarrow {AB} = \left( {1;4} \right)\) khi đó hệ số góc của đường thẳng \(AB\) là \(k = 4.\)
Đặt \(f\left( x \right) = {x^3} + \left( {m - 1} \right){x^2} - 3mx + 2m + 1\)
Để trên đồ thị hàm số có điểm mà tiếp tuyến tại đó vuông góc với đường thẳng \(AB\) thì hệ số góc tại tiếp điểm phải bằng \(k' = - \frac{1}{4}.\) Điều đó xảy ra khi và chỉ khi \(f'\left( x \right) = - \frac{1}{4}\) có nghiệm.
Ta có \(f'\left( x \right) = 3{x^2} + 2\left( {m - 1} \right)x - 3m.\)
Phương trình \(f'\left( x \right) = - \frac{1}{4} \Leftrightarrow 3{x^2} + 2\left( {m - 1} \right)x - 3m = - \frac{1}{4}\left( 1 \right).\)
Phương trình (1) có nghiệm khi \(\Delta ' \ge 0 \Leftrightarrow m \in \left( { - \infty ;\frac{{ - 7 - 4\sqrt 3 }}{2}} \right] \cup \left[ {\frac{{ - 7 + 4\sqrt 3 }}{2}; + \infty } \right).\)
Với \(\frac{{ - 7 + 4\sqrt 3 }}{2} \approx - 0,03\) nên các số nguyên dương \(m \in \left[ { - 2020;2020} \right]\) là \(\left\{ {1;2;3;...;2020} \right\}.\)
Vậy có 2020 số thỏa mãn yêu cầu bài toán.
Đáp án D
Cho hàm số \[f\left( x \right) = {x^3} - 3x + m\] ( với m là tham số thực). Biết \[\mathop {\max }\limits_{\left( { - \infty ;0} \right)} f\left( x \right) = 5\] . Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên \(\left( {0; + \infty } \right)\)là
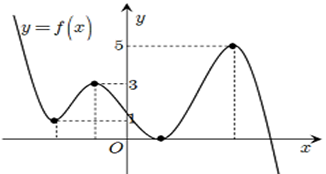
Cho hàm số\(y = f(x)\) liên tục trên\(\mathbb{R}\) và có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\frac{{{m^3} + 5m}}{{\sqrt {{f^2}(x) + 1} }} = {f^2}(x) + 6\) có đúng bốn nghiệm thực phân biệt.
Có bao nhiêu giá trị nguyên dương của tham số \(m\) không vượt quá 2020 để hàm số \(y = - {x^4} + (m - 5){x^2} + 3m - 1\) có ba điểm cực trị
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
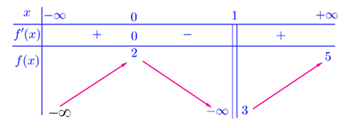
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
Mặt phẳng \[(AB'C')\] chia khối lăng trụ \[ABC.A'B'C'\] thành hai khối đa diện \[AA'B'C'\] và \[ABCC'B'\]có thể tích lần lượt là \[{V_1},\,{V_2}\]. Khẳng định nào sau đây đúng?
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'(x)\) có bảng biến thiên như hình dưới.

Bất phương trìnhn \(x.f\left( x \right) >mx + 1\) nghiệm đúng với mọi \(x \in \left[ {1;2020} \right)\) khi
Gọi S là tập hợp tất cả các số tự nhiên có 8 chữ số được lập từ các chữ số \(1;2;3;4;5;6\). Lấy ngẫu nhiên một số từ S. Xác suất chọn được số có ba chữ số 1, các chữ số còn lại xuất hiện không quá một lần và hai chữ số chẵn không đứng cạnh nhau bằng
Số giá trị nguyên của tham số thực \(m\) để hàm số \(y = \frac{{mx - 2}}{{ - 2x + m}}\) nghịch biến trên khoảng \(\left( {\frac{1}{2};\, + \infty } \right)\) là
Cho hàm số \(y = f(x)\) có bảng biến thiên như sau
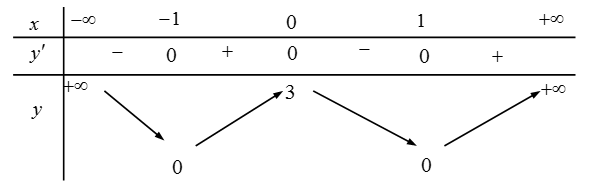
Khẳng định nào sau đây đúng?
Cho hàm số \[y = \frac{{x + m}}{{x + 1}}\] (\[m\] là tham số thực) thoả mãn \(\mathop {\min }\limits_{\left[ {1;2} \right]} y + \mathop {\max }\limits_{\left[ {1;2} \right]} y = \frac{9}{2}\). Mệnh đề nào dưới đây đúng?
Cho đa giác đều có 10 cạnh. Số tam giác có 3 đỉnh là ba đỉnh của đa giác đều đã cho là
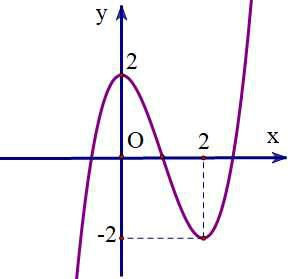
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Có bao nhiêu giá trị của tham số \(m\) để hàm số \(y = {x^3} + \frac{1}{2}({m^2} - 1){x^2} + 1 - m\) có điểm cực đại là \(x = - 1\)?
Cho hàm số \[y = f\left( x \right)\] xác định trên \(\mathbb{R}\backslash \left\{ 0 \right\}\) có bảng biến thiên như hình vẽ.
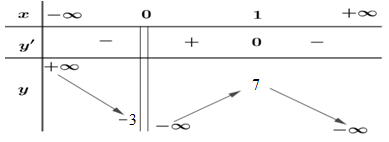
Số nghiệm của phương trình \[f(x) + 3 = 0\] là