Trong các khẳng định sau, khẳng định nào sai?

Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a, $\widehat{BAC} = {120}^0$, biết SA$\perp$(ABC) và mặt (SBC) hợp với đáy một góc ${45}^0$. Tính thể tích khối chóp S.ABC

Cho hình chóp S.ABCD có đáy là hình vuông ABCD tâm O có cạnh AB = a đường cao SO vuông góc với mặt đáy và SO = a. Khoảng cách giữa SC và AB là:

Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABCD) trung với trung điểm của AD;M  trung điểm CD; cạnh bên SB hợp với đáy góc ${60}^0$ . Thể tích của khối chóp S.ABM là

Cho hình chóp S.ABC có đáy là tam giác cân tại A, M là trung điểm của BC, J là trung điểm của BM, SA$\perp$đáy. Khẳng định nào sau đây là đúng?

Cho hình chóp S.ABCD đáy ABCD là hình chữ nhật: AB = 2a, AD = a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB;SC tạo với đáy góc ${45}^0$ . Khoảng cách từ A đến mặt phẳng (SCD) là

Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = b, SA vuông góc với đáy, SA = 2a. Điểm M thuộc đoạn SA, AM = x. Giá trị của x để mặt phẳng (MBC) chia khối S.ABCD thành hai khối có thể tích bằng nhau là:

Cho tứ diện ABCD, gọi I, J, K lần lượt là trung điểm của AC, BC, BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là:

Cho hình chóp S.ABCD có AC = 2a, mặt bên (SBC) tạo bởi mặt đáy (ABCD) một góc ${45}^0$ . Tính thể tích V của khối chóp S.ABCD

Cho một tấm nhôm hình chữ nhật ABCD có AD = 60 cm. Ta gập tấm nhôm theo 2 cạnh MN và PQ vào phía trong đến khi AB và DC trùng nhau như hình vẽ dưới đây để được một hình lăng trụ khuyết 2 đáy.

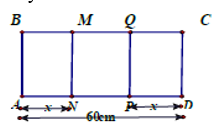
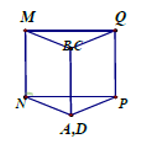
Tìm x để thể tích khối lăng trụ lớn nhất?

Cho hình lăng trụ tứ giác ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a và thể tích bằng $3a^3$ . Tính chiều cao h của hình lăng trụ đã cho.

Hình bát diện đều có tất cả bao nhiêu cạnh

Trong các  mệnh đề sau, mệnh đề nào đúng?

Cho tứ diện ABCD . Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ diện AB'C'D' và khối tứ diện ABCD bằng: