Cho hình chóp S.ABCD đáy ABCD là hình chữ nhật: AB = 2a, AD = a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB;SC tạo với đáy góc . Khoảng cách từ A đến mặt phẳng (SCD) là
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
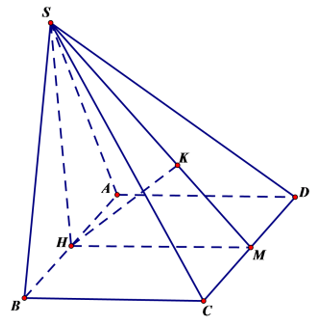
Gọi M là trung điểm của CD. Kẻ HK vuông góc với SM.
Ta có:
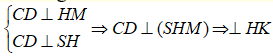
Mặt khác ta có HKSM
Suy ra HK(SCD)
Vậy ![]()
Xét tam giác BHC vuông tại B, ta có:
![]()
![]()
Xét tam giác SHM vuông tại H, ta có:
![]()
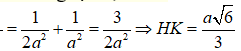
Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a, , biết SA(ABC) và mặt (SBC) hợp với đáy một góc . Tính thể tích khối chóp S.ABC
Cho hình chóp S.ABCD có đáy là hình vuông ABCD tâm O có cạnh AB = a đường cao SO vuông góc với mặt đáy và SO = a. Khoảng cách giữa SC và AB là:
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABCD) trung với trung điểm của AD;M trung điểm CD; cạnh bên SB hợp với đáy góc . Thể tích của khối chóp S.ABM là
Cho hình chóp S.ABC có đáy là tam giác cân tại A, M là trung điểm của BC, J là trung điểm của BM, SAđáy. Khẳng định nào sau đây là đúng?
Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = b, SA vuông góc với đáy, SA = 2a. Điểm M thuộc đoạn SA, AM = x. Giá trị của x để mặt phẳng (MBC) chia khối S.ABCD thành hai khối có thể tích bằng nhau là:
Cho tứ diện ABCD, gọi I, J, K lần lượt là trung điểm của AC, BC, BD. Giao tuyến của hai mặt phẳng (ABD) và (IJK) là:
Cho hình chóp S.ABCD có AC = 2a, mặt bên (SBC) tạo bởi mặt đáy (ABCD) một góc . Tính thể tích V của khối chóp S.ABCD
Cho một tấm nhôm hình chữ nhật ABCD có AD = 60 cm. Ta gập tấm nhôm theo 2 cạnh MN và PQ vào phía trong đến khi AB và DC trùng nhau như hình vẽ dưới đây để được một hình lăng trụ khuyết 2 đáy.
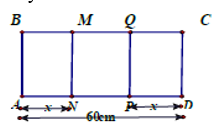
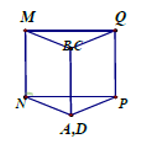
Tìm x để thể tích khối lăng trụ lớn nhất?
Cho hình lăng trụ tứ giác ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a và thể tích bằng . Tính chiều cao h của hình lăng trụ đã cho.
Cho tứ diện ABCD . Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ diện AB'C'D' và khối tứ diện ABCD bằng: