Cho hình thang ABDC (AB // CD). Trên cạnh AD lấy điểm M và N sao cho AM = MN = NC. Từ M và N kẻ các đường thẳng song song với hai đáy cắt BC theo thứ tự E và F. Chứng minh rằng:
a. BE = EF = FD
b. Cho CD = 8cm, ME = 6cm. Tính độ dài AB và FN
Giải bởi Vietjack
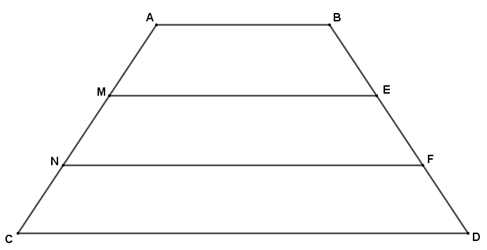
a. Ta có ABCD là hình thang AB // CD
Ta có AB // CD, FN // CD suy ra AB // NF
Vậy ABFN là hình thang (dấu hiệu nhận biết).
Xét hình thang ABFN có ME // NF, ME = NF nên ME là đường trung bình của hình thang ABFN
Suy ra BE = EF.
Xét tương tự với hình thang MEDC ta suy ra EF = FD
Ta có điều phải chứng minh.
b. Theo chứng minh trên ta có
Chứng minh biểu thức sau không phụ thuộc vào x
a. A = (2x - 1)(4x2 + 2x + 1) - (2x + 1)(4x2 - 2x + 1)
b. B = x(2x + 1) - x2(x + 2) + x3 - x + 5
Tính giá trị nhỏ nhất của biểu thức P = x2 - 2xy + 6y2 - 12x + 2y + 45
a. 8x2 - 8xy - 4x + 4y
b. x3 + 10x2 + 25x - xy2
c. x2 + x - 6
d. 2x2 + 4x - 16
Tìm giá trị của x, biết:
a. x3 - 16x = 0
b. (2x + 1)2 - (x - 1)2 = 0
