A. 2.
B. 3.
C. 1.
D. 4.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Xét hàm số g (x) = x2 - 4x - 1 + m
Ta có:
+ TH1: Phương trình (*) không cho nghiệm mũ lẻ. Suy ra f (x) chỉ có một cực trị x = 2
Điều kiện: D = (-2)2 - (-1 + m) = 5 - m 0
m ³ 5
Ta xét bảng biến thiên của hàm số y = f (x) trên đoạn [0; 3]
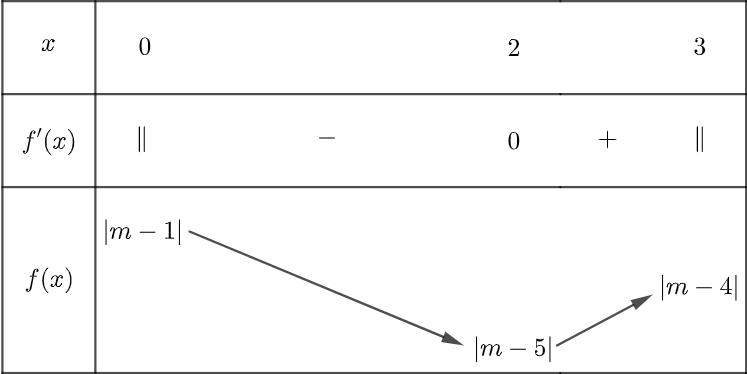
Với m ³ 5
Vậy
Û m = 4 (loại).
+ TH1: Phương trình (*) cho 2 nghiệm mũ lẻ. Suy ra f (x) chỉ có 3 cực trị x = 2, x = x1 và x= x2
Điều kiện: D = (-2)2 - (-1 + m) = 5 - m > 0
m < 5
Ta xét bảng biến thiên của hàm số y = f (x) trên đoạn [0; 3]
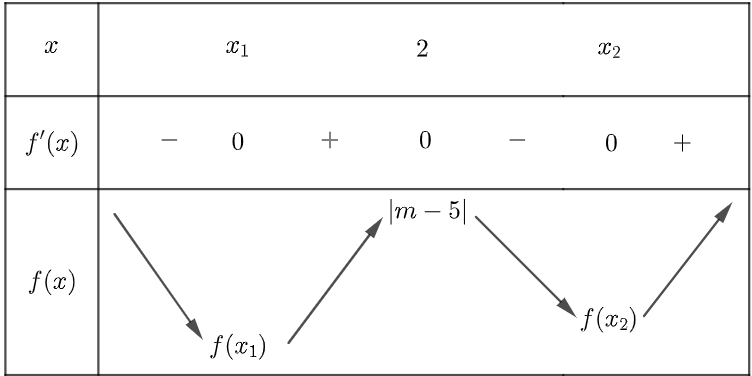
Với m < 5 nên f(2) > f (0) > f (3)
Kết hợp với dựa vào bảng biến thiên thì f (2) > f (x1) và f (x2)
Nên
m = 2 (thỏa mãn)
Vậy chỉ có 1 giá trị của m thỏa mãn điều kiện bài toán là m = 2.
Trong mặt phẳng tọa độ Oxy, gọi (C) là đồ thị của hàm số . Phương trình tiếp tuyến của (C) tại giao điểm của đồ thị (C) với trục hoành là
Trong không gian tọa độ Oxyz, gọi (P) là mặt phẳng đi qua 2 điểm A(0; 1; -2), B(2; 1; 0) sao cho khoảng cách từ gốc tọa độ O đến (P) lớn nhất. Phương trình của mặt phẳng (P) là
Trong mặt phẳng tọa độ Oxy, gọi A, B, C, D là 4 điểm cực trị của đồ thị hàm số với hoành độ đều khác 0. Bán kính đường tròn ngoại tiếp đi qua 4 điểm A, B, C, D bằng
Cho hàm số f (x) liên tục và có đạo hàm trên [0; 1]. Biết và f (0) = f (1) = 7. Giá trị của tích phân bằng
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD và điểm O tùy ý trên mặt phẳng (BCD). Thể tích tứ diện OMNP bằng