Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 5)
-
5697 lượt thi
-
50 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Trong không gian tọa độ Oxyz, có vectơ .
Do đó tọa độ của .
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Cho hàm số y = f (x) = x3 - 3x - 2022
Để hàm số y = f (x) nghịch biến thì
Vậy hàm số y = x3 - 3x - 2022 nghịch biến trên khoảng (-1; 1).
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Công thức tính diện tích xung quanh của hình nón với bán kính mặt đáy r và độ dài đường sinh l là:
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Khối lập phương là khối đa diện đều loại {4; 3}.
Câu 6:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
x.(x - 1) - 3.(x - 1) = 0
(x - 1).(x - 3) = 0
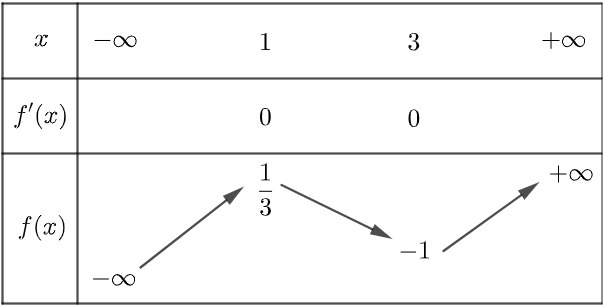
Dựa vào bảng biến thiên. Suy ra, điểm cực đại của hàm số là x = 3.
Câu 7:
Tập xác định của hàm số là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hàm số xác định khi và chỉ khi x - 1 > 0 x > 1
Vậy tập xác định của hàm số là D = (1; +).
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án đúng là D.
Mặt cầu tâm O(0; 0; 0), bán kính bằng 2 có phương trình là
(x - 0)2 + (y - 0)2 + (z - 0)2 = 22
x2 + y2 + z2 = 4.
Câu 11:
Trong không gian tọa độ Oxyz, cho . Giá trị của tích vô hướng bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tích vô hướng
= 1.(-1) + (-2).2 + 2.1 = (-1) + (-4) + 2 = -3
Câu 12:
Phương trình đường tiệm cận ngang của đồ thị hàm số là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Phương trình đường tiệm cận ngang của đồ thị hàm số là
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Phương trình mặt phẳng đi qua điểm M(-1; 2; 1) và nhận vectơ làm vectơ pháp tuyến là
2.[x - (-1)] + (-1).(y - 2) + (-1).(z - 1) = 0
2(x + 1) + (y - 2) + (z - 1) = 0
2x + 2 - y + 2 - z + 1 = 0
2x - y - z + 5 = 0.
Câu 15:
Tập xác định của hàm số là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hàm số xác định khi và chỉ khi
Vậy tập xác định của hàm số là D = (0; +) \ {2}.
Câu 17:
Trong mặt phẳng tọa độ Oxy, gọi (C) là đồ thị của hàm số . Phương trình tiếp tuyến của (C) tại giao điểm của đồ thị (C) với trục hoành là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình giao điểm của đồ thị (C) với trục hoành là
Vậy tọa độ giao điểm của đồ thị (C) với trục hoành là I(1; 0)
Phương trình tiếp tuyến của (C) tại giao điểm I(1; 0) là
y = (-1).(x - 1) + 0
y = 1 - x.
Câu 18:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
P = log6 12 = log6 (6.2) = log6 6 + log6 2
.
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Công thức tính thể tích khối tròn xoay tạo thành khi quay quanh trục Ox hình phẳng giới hạn bởi (C), trục hoành, đường thẳng x = a và x = b là .
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
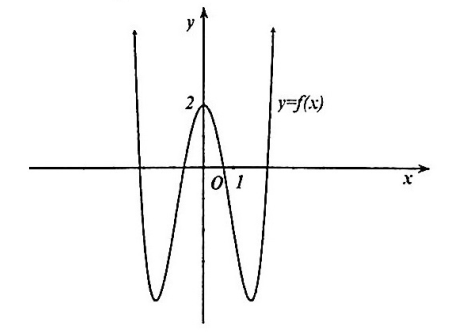
Nhận dạng đồ thị trên là đồ thị của hàm trùng phương y = f (x) = ax4 + bx2 + c (a ¹ 0)
Đồ thị f (x) đi qua điểm có tọa độ (0; 2) nên ta có f (0) = c = 2.
Suy ra f (x) = ax4 + bx2 + 2
Từ đó,
Dựa vào đồ thị ta thấy, khi x ⟶ + thì f (x) ⟶ +
Từ đó suy ra a > 0
Loại 2 đáp án là A và D
Ngoài cực trị x = 0, f (x) còn tồn tại hai cực trị trái dấu x1, x2 với
Nên suy ra a.b < 0
Loại đáp án B
Vậy đồ thị hàm số thỏa mãn những điều kiện trên là y = x4 - 5x2 + 2.
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
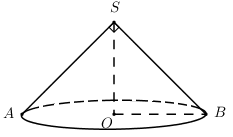
Ta có: SA = SB = a = l
Tam giác SAB là tam giác vuông cân tại S.
Theo định lý Py-ta-go với tam giác SAB vuông cân tại S, ta có:
Và
Thể tích khối nón bằng .
Câu 22:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
6x + 12 = 3x+1 + 2x+2
6x + 12 = 3.3x + 4.2x
6x - 3.3x = 4.2x - 12
3x.(2x - 3) = 4.(2x - 3)
(3x - 4).(2x - 3) = 0
Từ đó x1.x2 = log3 4.log2 3 = log2 4 = 2.
Câu 25:
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 4sin3 x + 9cos2 x + 6sin x -10. Giá trị của tích M.m bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
y = 4sin3 x + 9cos2 x + 6sin x - 10
= 4sin3 x + (9cos2 x - 9) + 6sin x - 1
= 4sin3 x - 9sin2 x + 6sin x - 1
Đặt f (t) = 4t3 - 9t2 + 6t - 1 với t = sin x Î [-1; 1]
(12t2 -12t) - (6t - 6) = 0
12t.(t - 1) - 6(t - 1) = 0
6(2t -1).(t - 1) = 0
Xét bảng biến thiên của hàm số f (t) = 4t3 - 9t2 + 6t - 1 trên đoạn [-1; 1]
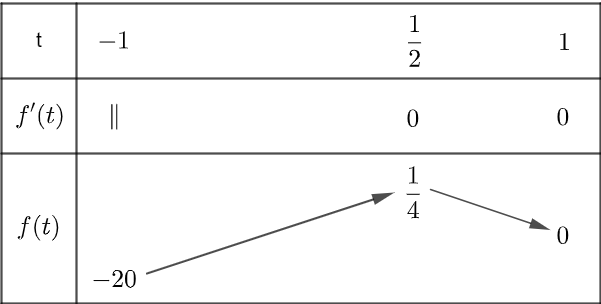
Dựa vào bảng biến thiên, suy ra
Do đó
Câu 26:
Gọi F (x) là một nguyên hàm của hàm số f (x) = ex thỏa mãn F (0) = 2. Giá trị của F (1) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
F (0) = e0 + C = 1 + C = 2
C = 1 F (x) = ex + 1
Suy ra, F (1) = e + 1.
Câu 28:
Tất cả các giá trị của tham số m để hàm số đồng biến trên khoảng (-; -2) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hàm số đồng biến trên khoảng khi và chỉ khi
Vậy giá trị thỏa mãn yêu cầu bài toán.
Câu 30:
Cho F (x) là một nguyên hàm của hàm số f (x) = x.(x2 + 1)2022 thỏa mãn . Giá trị của F (1) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đặt u = x2 + 1 du = 2xdx
Từ đó
Câu 31:
Gọi a, b là các số nguyên dương nhỏ nhất sao cho . Giá trị của a + b.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Suy ra a = 3, b = 4
Vậy giá trị a + b = 3 + 4 = 7.
Câu 32:
Trong không gian tọa độ Oxyz, cho 2 điểm A(-1; 2; 0), B(3; 2; 2). Phương trình mặt phẳng trung trực của đoạn AB là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi I là trung điểm của đoạn thẳng AB với A(-1; 2; 0), B(3; 2; 2)
Suy ra điểm I có tọa độ là (xI; yI; zI) với
I(1; 2; 1)
Ta có
Mặt phẳng trung trực của đoạn thẳng AB nhận vectơ là vectơ pháp tuyến
Mặt phẳng (P) đi qua điểm I(1; 2; 1), nhận là vectơ pháp tuyến có phương trình
4(x - 1) + 2(z - 1) = 0
4x - 4 + 2z - 2 = 0
4x + 2z - 6 = 0
2x + z - 3 = 0.
Câu 33:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đặt
Đổi cận ta được:
+ x = 0 u = 1
+ x = 2 u = 2
Suy ra
a = 1, b = -2
a2 + b2 = 12 + (-2)2 = 5.
Câu 34:
Gọi a, b là các số hữu tỉ sao cho . Giá trị của tích ab bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đặt x = tan t Þ x2 + 1 = tan2 t + 1
Và
Đổi cận ta được:
+ x = 0 t = 0
+ x = 2
Suy ra
Câu 35:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phương trình hoành độ giao điểm của đồ thị hàm số y = x3 và trục hoành là x3 = 0 x = 0
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x3, trục hoành và đường thẳng x = 1 là
Câu 36:
Một xe ô tô đang đi với vận tốc 10 m/s thì người lái xe bắt đầu đạp phanh, từ thời điểm đó xe chuyển động chậm dần đều với vận tốc v (t) = 10 - 5t (m/s), ở đó t tính bằng giây. Quãng đường ô tô dịch chuyển từ lúc đạp phanh đến lúc dừng hẳn bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Từ thời điểm t0 = 0 (s) đến lúc dừng hẳn tức là v (t1) = 10 - 5t1 = 0 t1 = 2 (s)
Quãng đường ô tô dịch chuyển từ lúc đạp phanh đến lúc dừng hẳn bằng
(m).
Câu 37:
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD và điểm O tùy ý trên mặt phẳng (BCD). Thể tích tứ diện OMNP bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
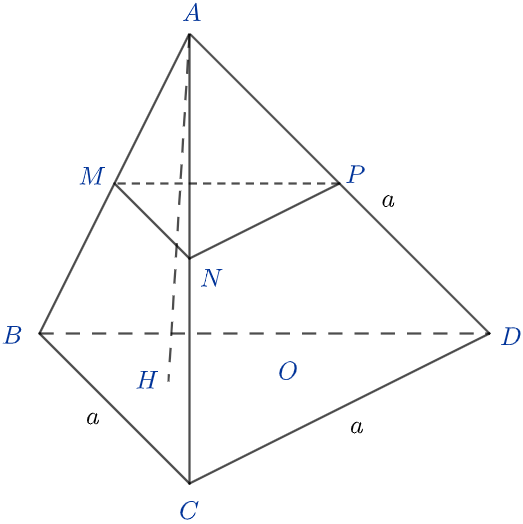
AH là đường cao của tứ diện đều A.BCD nên H là trọng tâm tam giác BCD
Suy ra,
Và
Ta có:
Suy ra mặt phẳng (MNP) song song với mặt phẳng (BCD)
dO/(MNP) = dB/(MNP) = dA/(MNP)
Suy ra
Câu 38:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
x.log28 2 + y.log28 7 = 2
(*)
Đặt log7 2 = t nên suy ra phương trình (*) trở thành
(**)
Với x, y là hai số tự nhiên thì phương trình (**) chỉ thỏa mãn khi và chỉ khi x = 2.2 = 4 và y = 2.1 = 2
x + y = 4 + 2 = 6.
Câu 39:
Cho hình chóp S.ABC có SA (ABC), và . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
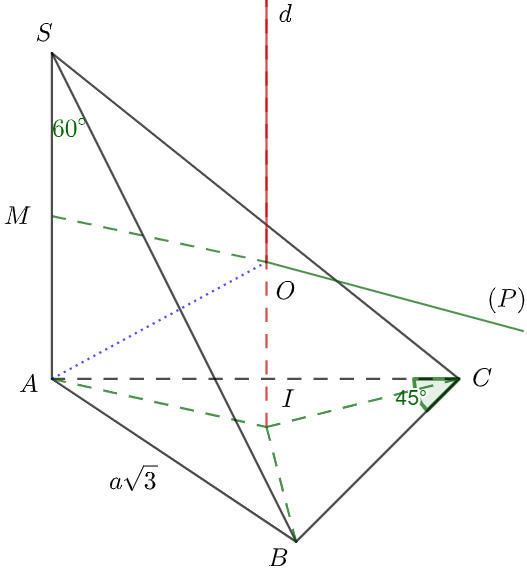
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng định lý sin ta có
Từ tâm I dựng đường thẳng d vuông góc với mặt đáy.
Lấy M là trung điểm của SA, tạo một mặt phẳng (P) qua M sao cho SA (P)
Mặt phẳng (P) cắt đường thẳng d tại một điểm O, đó là tâm mặt cầu cần tìm và độ dài AO chính là bán kính mặt cầu đó
Áp dụng định lý Pytago vào tam giác OAM vuông tại M
Câu 40:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
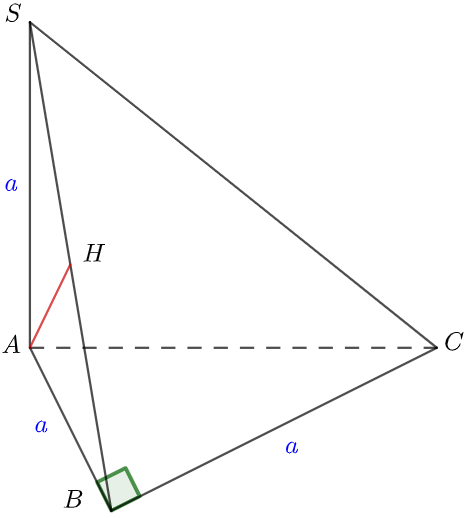
Ta có SA (ABC) Þ SA BC
Kết hợp điều kiện AB BC (Do )
Suy ra BC (SAB)
Kẻ AH SB (H SB) (*)
Þ BC AH (**)
Từ (*) và (**) nên suy ra AH (SBC)
Vậy khoảng cách từ A đến mặt phẳng (SBC) chính bằng AH
Áp dụng hệ thức lượng trong tam giác SAB vuông tại A ta có
Câu 41:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
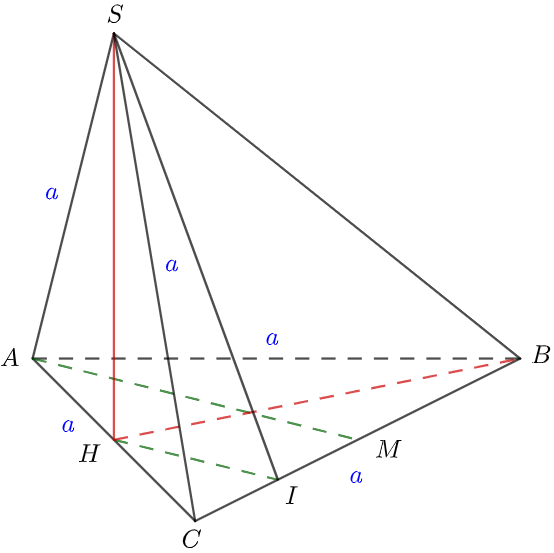
Lấy H là trung điểm của AC và tam giác ABC, tam giác SAC đều nên ta có SH AC, BH AC
(SAC) (ABC)
Tam giác ABC đều nên với M là trung điểm của BC thì ta có AM BC
Kẻ HI // AM (I BC) HI BC (*)
Kết hợp điều kiện SH BC (Do SH (ABC))
Nên suy ra BC (SHI) BC SI (**)
Từ (*) và (**) nên góc giữa hai mặt phẳng (ABC) và (SBC) chính là góc
Xét tam giác SIH vuông tại H ta có
SH và AM là đường cao của tam giác đều có cạnh bằng a nên
Từ đó suy ra
Câu 42:
Trong không gian tọa độ Oxyz, cho A(-1; 2; 2), B(2; -1; -2). Diện tích tam giác OAB bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có:
Diện tích tam giác OAB được tính theo công thức
Câu 43:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi I là trung điểm của đoạn thẳng AB với A(-1; 2; 0), B(-3; 4; 2)
Suy ra điểm I có tọa độ là (xI; yI; zI) với
I(-2; 3; 1)
Mặt cầu tâm I(-2; 3; 1) và bán kính có phương trình
(x + 2)2 + (y - 3)2 + (z - 1)2 = 3.
Câu 44:
Trong không gian tọa độ Oxyz, gọi (P) là mặt phẳng đi qua 2 điểm A(0; 1; -2), B(2; 1; 0) sao cho khoảng cách từ gốc tọa độ O đến (P) lớn nhất. Phương trình của mặt phẳng (P) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi phương trình mặt phẳng (P) có dạng Ax + By + Cz + D = 0
Hai điểm A(0; 1; -2), B(2; 1; 0) thuộc mặt phẳng (P) nên ta có hệ phương trình
Phương trình (P) trở thành
Khoảng cách từ O đến (P) là
(*)
+ Với D = 0 dO/(P) = 0
+ Với D 0. Chia cả tử và mẫu của (*) cho ta được
với
Yêu cầu bài toán tìm t ℝ để đạt giá trị lớn nhất
Suy ra hàm số đạt giá trị nhỏ nhất
Bài toán thỏa mãn khi và chỉ khi t đạt tại giá trị
Với
Chọn B = 1, D = -3 A = - C = 1
Suy ra phương trình mặt phẳng (P) là
x + y - z - 3 = 0.
Câu 45:
Cho hàm số f (x) liên tục và có đạo hàm trên [0; 1]. Biết và f (0) = f (1) = 7. Giá trị của tích phân bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có:
Câu 46:
Trong không gian Oxyz, cho hai điểm A(-1; 0; 2), B(3; 2; -2). Biết tập hợp các điểm M thỏa mãn MA2 + MB2 = 30 là một mặt cầu. Bán kính mặt cầu đó bằng
 Xem đáp án
Xem đáp án
Gọi điểm M có tọa độ là M(x; y; z)
MA2 + MB2 = 30
Û (x + 1)2 + y2 + (z – 2)2 + (x – 3)2 + (y – 2)2 + (z + 2)2 = 30
Û x2 + 2x + 1 + y2 + z2 – 4z + 4 + x2 – 6x + 9 + y2 – 4y + 4 + z2 + 4z + 4 = 30
2x2 + 2y2 + 2z2 – 4x – 4y – 8 = 0
x2 + y2 + z2 – 2x – 2y – 4 = 0
(x2 – 2x + 1) + (y2 – 2y + 1) + z2 = 6
(x – 1)2 + (y – 1)2 + z2 = 6 (*)
Phương trình (*) là phương trình một mặt cầu có bán kính
Câu 47:
Cho phương trình với tham số m. Số giá trị nguyên dương của m để phương trình đã cho có nghiệm là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Tập xác định
Đặt t = log2 (x + 1) (t Î ℝ \ {0})
Phương trình (*) trở thành
t2 + 4m = 5t (Nhân 2 vế với t)
t2 – 5t = –4m
Xét bảng biến thiên của f (t) = t2 – 5t = –4m trên ℝ \ {0}
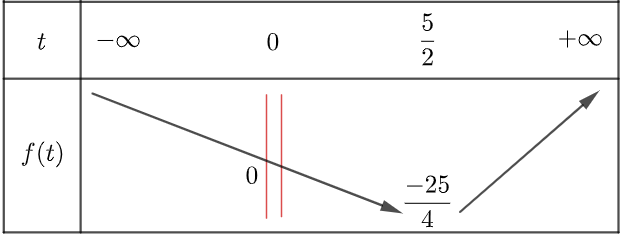
Dựa vào bảng biên thiên để phương trình có nghiệm thì
Số giá trị nguyên dương của m là m = {1}
Câu 48:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét hàm số g (x) = x2 - 4x - 1 + m
Ta có:
+ TH1: Phương trình (*) không cho nghiệm mũ lẻ. Suy ra f (x) chỉ có một cực trị x = 2
Điều kiện: D = (-2)2 - (-1 + m) = 5 - m 0
m ³ 5
Ta xét bảng biến thiên của hàm số y = f (x) trên đoạn [0; 3]
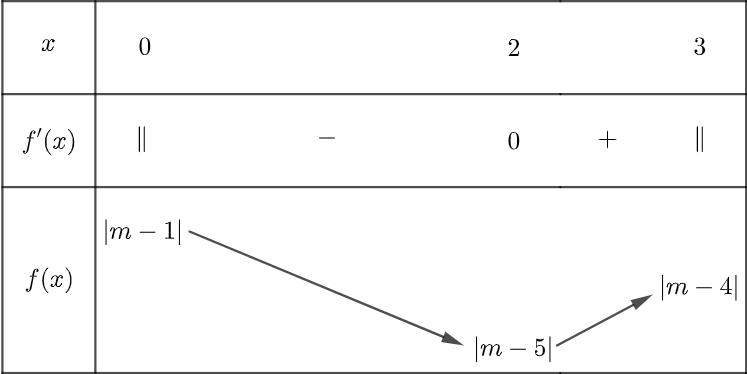
Với m ³ 5
Vậy
Û m = 4 (loại).
+ TH1: Phương trình (*) cho 2 nghiệm mũ lẻ. Suy ra f (x) chỉ có 3 cực trị x = 2, x = x1 và x= x2
Điều kiện: D = (-2)2 - (-1 + m) = 5 - m > 0
m < 5
Ta xét bảng biến thiên của hàm số y = f (x) trên đoạn [0; 3]
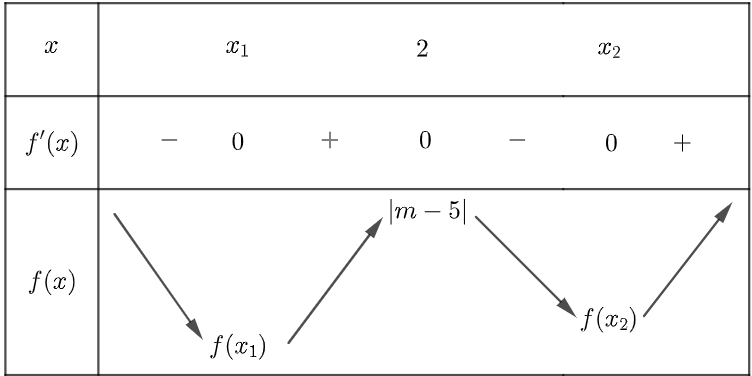
Với m < 5 nên f(2) > f (0) > f (3)
Kết hợp với dựa vào bảng biến thiên thì f (2) > f (x1) và f (x2)
Nên
m = 2 (thỏa mãn)
Vậy chỉ có 1 giá trị của m thỏa mãn điều kiện bài toán là m = 2.
Câu 49:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
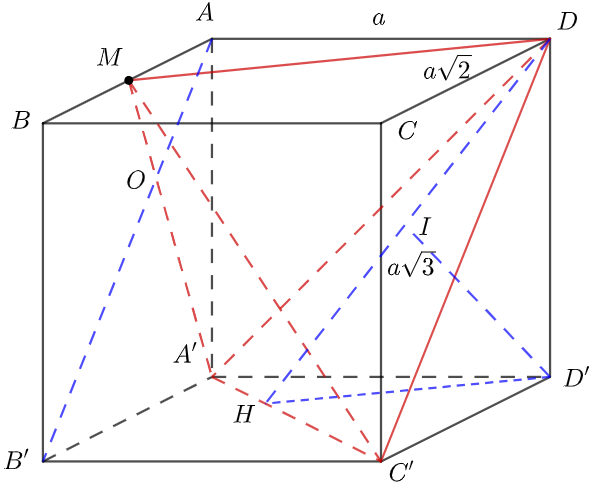
Áp dụng định lý Pytago ta có
Sử dụng công thức Hê-rông tính diện tích tam giác A’DC’
Ta có p là nửa chu vi tam giác A’DC’ với
Suy ra (*)
Thay các giá trị vào (*) ta được
Kẻ D’H A’C’ (H A’C’)
D’I DH (I DH)
Vậy khoảng cách từ D’ đến A’DC’ chính bằng ID’
Áp dụng hệ thức lượng trong tam giác vuông ta có
Lại có, MA // A’B’ nên theo Ta-lét ta có
Kết hợp điều kiện AB’ // DC’
2dM/(A’DC’) = 3dO/(A’DC’)
= 3dA/(A’DC’) = 3dD’/(A’DC’) = 3ID’
Suy ra
Câu 50:
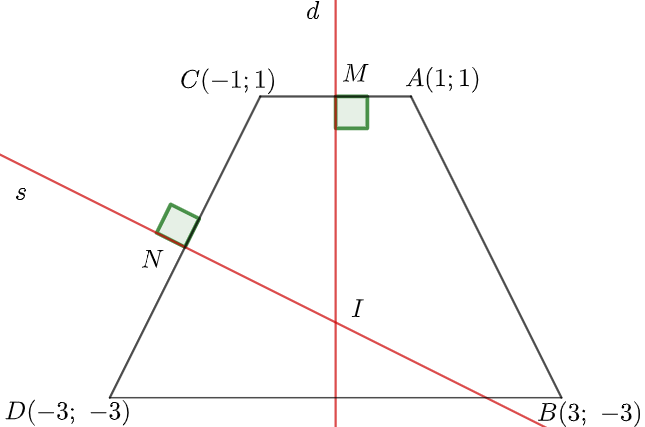
Trong mặt phẳng tọa độ Oxy, gọi A, B, C, D là 4 điểm cực trị của đồ thị hàm số với hoành độ đều khác 0. Bán kính đường tròn ngoại tiếp đi qua 4 điểm A, B, C, D bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
+ Với x > 0 y = x3 - 6x2 + 9x - 3
(3x2 - 9x) - (3x - 9) = 0
3x.(x - 3) - 3(x - 3) = 0
3(x - 1).(x - 3) = 0
Suy ra xA = 1 thì tọa độ điểm A là (1; 1)
xB = 3 thì tọa độ điểm B là (3; -3)
+ Với x < 0 y = - x3 - 6x2 - 9x - 3
(- 3x2 - 9x) - (3x + 9) = 0
-3x.(x + 3) - 3(x + 3) = 0
-3(x + 1).(x + 3) = 0
Suy ra xC = -1 thì tọa độ điểm C là (-1; 1)
xD = 3 thì tọa độ điểm D là (-3; -3)
d là trục đối xứng của hình thang cân ABDC nên với mọi điểm nằm trên d luôn cách đều hai điểm A, C và hai điểm B, D (*)
Suy ra d là đường trung trực của hai đoạn thẳng AC và BD, cắt AC tại M
M là trung điểm của AC nên ta có tọa độ điểm M là M(xM; yM) với
Þ M(0; 1)
Kẻ đường thẳng s là đường trung trực của đoạn thẳng CD, cắt CD và d lần lượt tại N và I
Suy ra với mọi điểm trên s thì cách đều hai điểm C và D (**)
N là trung điểm của CD nên tương tự ta có tọa độ điểm N là N(-2; -1)
Từ (*) và (**) suy ra I là tâm đường tròn ngoại tiếp hình thang cân ABDC
Đường thẳng d đi qua M(0; 1) và có vectơ pháp tuyến là có phương trình (d): 2x = 0
I(0; yI)
Đường thẳng s đi qua N(-2; -1) và có vectơ pháp tuyến là có phương trình
2(x + 2) + 4(y+1) = 0
2x + 4 + 4y + 4 = 0
2x + 4y + 8 = 0
x + 2y + 4 = 0
Từ đây suy ra xI + 2yI + 4 = 0 Û yI = -2
Suy ra tọa độ điểm I là I(0; -2)
Vậy bán kính đường tròn ngoại tiếp ABDC là
