Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 2)
-
5388 lượt thi
-
35 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 4:
Một nguyên hàm của hàm số là:
 Xem đáp án
Xem đáp án
Câu 6:
Một nguyên hàm của là kết quả nào sau đây, biết nguyên hàm này triệt tiêu khi x= 1 ?
 Xem đáp án
Xem đáp án
Câu 7:
 Xem đáp án
Xem đáp án
Chọn C
Phương án C cần sửa thành:Câu 16:
 Xem đáp án
Xem đáp án
Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số và là:Câu 17:
Cho hàm số f(x) liên tục trên R và với mọi xR. Giá trị của tích phân là
 Xem đáp án
Xem đáp án
Chọn B.
Đặt t = - x suy ra: dt = -dxCâu 18:
Diện tích hình phẳng giới hạn bởi có kết quả là
 Xem đáp án
Xem đáp án
Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số và là:Câu 19:
Thể tích của khối tròn xoay được giới hạn bởi đồ thị hàm số liên tục trên đoạn trục Ox và hai đường thẳng quay quanh trục Ox, có công thức là:
 Xem đáp án
Xem đáp án
Chọn B.
Áp dụng công thức tính thể tích khối tròn xoay: giới hạn bởi đồ thị hàm số , trục Ox, x = a, x = b khi quay xung quanh trục Ox ta có:
Câu 20:
Hình (S) giới hạn bởi . Tính thể tích khối tròn xoay khi quay hình (S) quanh trục Ox.
 Xem đáp án
Xem đáp án
Chọn C.
Phương trình hoành độ giao điểm:Câu 21:
Cho hàm số f(x) xác định trên và thỏa mãn: . Biết rằng và . Tính
 Xem đáp án
Xem đáp án
Chọn C
Ta có
Với ;
Với ;
Mà
Do đó ;
Với ;
Mà
Do đó với ;
Vậy
Câu 22:
Đồ thị của hàm số trên đoạn [-3;5] như hình vẽ dưới đây(phần cong của đồ thị là một phần của Parabol ). Tính
![Đồ thị của hàm số y = f(x) trên đoạn [-3;5] như hình vẽ dưới đây (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/06/2-1654273078.png)
 Xem đáp án
Xem đáp án
![Đồ thị của hàm số y = f(x) trên đoạn [-3;5] như hình vẽ dưới đây (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2022/06/1-1654272913.png)
Câu 23:
Trong không gian với hệ trục tọa độ Oxyz cho A(0;-1;1) , B(-2;1;-1) , C(-1;3;2) . Biết rằng ABCDlà hình bình hành, khi đó tạo độ điểm D là
 Xem đáp án
Xem đáp án
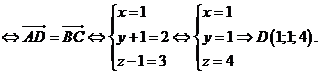
Câu 24:
 Xem đáp án
Xem đáp án
Chọn B.
Ta có M(1;-2;5) , suy ra hình chiếu vuông góc của M trên mặt phẳng (Oxy) là M'(1;-2;0).
Câu 25:
Trong không gian với hệ trục tọa độ Oxyz, cho và , 4. Khi đó có giá trị bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn B.
Ta có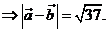
Câu 26:
 Xem đáp án
Xem đáp án
Chọn C
Ta có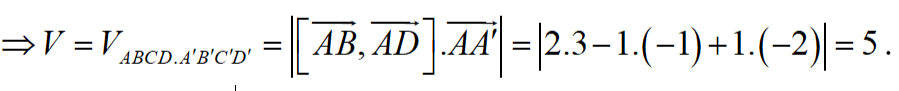
Câu 27:
 Xem đáp án
Xem đáp án
Chọn D
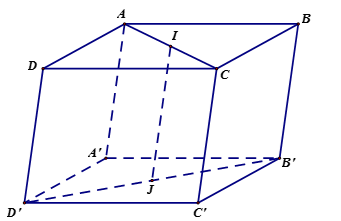
Câu 28:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm ![]() . Kí hiệu điểm M thuộc tia đối của tia BA sao cho
. Kí hiệu điểm M thuộc tia đối của tia BA sao cho ![]() . Tọa độ của điểm M là
. Tọa độ của điểm M là
 Xem đáp án
Xem đáp án
Chọn C
Gọi ![]() . Theo yêu cầu bài toán:
. Theo yêu cầu bài toán: ![]()
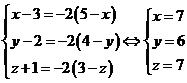
Câu 29:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm . Với giá trị nào của x và y thì ba điểm A, B, M thẳng hàng?
 Xem đáp án
Xem đáp án
Chọn D.
Ta có:Câu 31:
Cho hai vectơ . Góc giữa chúng bằng khi:
 Xem đáp án
Xem đáp án
Câu 32:
Trong không gian với hệ toạ độ Oxyz, cho ba điểm . Để ba điểm A, B, C thẳng hàng thì tổng giá trị 5x + y là:
 Xem đáp án
Xem đáp án
Chọn A.
Có