Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 3)
-
5833 lượt thi
-
35 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 5:
Hàm số có một nguyên hàm F(x) là kết quả nào sau đây, biết nguyên hàm này bằng 1 khi x= 0?
 Xem đáp án
Xem đáp án
Chọn D.
Giả sửCâu 7:
 Xem đáp án
Xem đáp án
Chọn D.
Câu 8:
Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn . Biết rằng , , , và . Tích phân có giá trị bằng
 Xem đáp án
Xem đáp án
Chọn A.
Áp dụng công thức tích phân từng phần, ta cóCâu 16:
Cho hàm số f(x) liên tục trên R và với mọi xR. Giá trị của tích phân là
 Xem đáp án
Xem đáp án
Chọn B.
ĐặtCâu 17:
 Xem đáp án
Xem đáp án
Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số và là :Ta có:
Do đó:Câu 18:
 Xem đáp án
Xem đáp án
Chọn D.
Phương trình hoành độ giao điểm của hai đồ thị hàm số và là:Câu 19:
 Xem đáp án
Xem đáp án
Chọn A.
Thể tích khối tròn xoay được giới hạn bởi các đường và x= 1 khi quay quanh trục Ox là:Câu 20:
 Xem đáp án
Xem đáp án
Chọn C.
Phương trình hoành độ giao điểm:
Suy ra:Câu 21:
 Xem đáp án
Xem đáp án
Đáp án B
Đặt
Đổi cậnLúc đó
Suy ra
Do đó
Cách 2: Chọn là một hàm thỏa các giả thiết. Dễ dàng tính đượcCâu 22:
 Xem đáp án
Xem đáp án
Chọn C
- Tính :
Tính
Đặt- Kết hợp giả thiết ta được :
- Mặt khác, ta tính được :
- Cộng vế với vế các đẳng thức (1), (2), (3) ta được:Câu 23:
 Xem đáp án
Xem đáp án
Chọn A
Ta có là véctơ cùng phương với ![]()
Suy ra ![]()
Câu 24:
Trong không gian với hệ tọa độ Oxyz , cho A(2;9;-1) , B(0;4;1) , C(m;2m+5;1) . Biết là giá trị để tam giác ABC vuông tại C Khi đó giá trị gần giá trị nào nhất trong các giá trị sau?
 Xem đáp án
Xem đáp án
Chọn A
Ta có 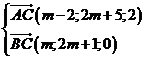
Do tam giác ABC vuông tại C
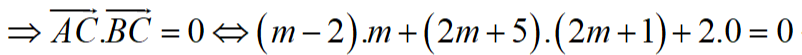
Câu 25:
 Xem đáp án
Xem đáp án
Chọn A.
Ta có (P) tiếp xúc với 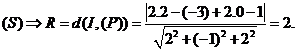
Câu 26:
 Xem đáp án
Xem đáp án
Chọn A.
Ta có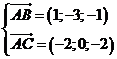
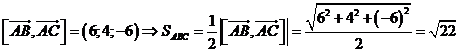
Câu 27:
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có A(0;-1;1) , B(-2;1;1) , C(-1;0;0) , D(1;1;1) . Thể tích V của tứ diện ABCD bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn D.
Ta có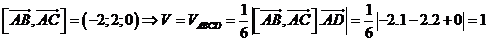
Câu 29:
 Xem đáp án
Xem đáp án
Chọn C.
Ta có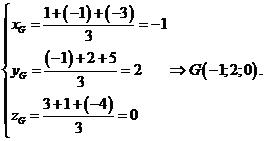
Câu 30:
 Xem đáp án
Xem đáp án
Chọn C.
Gọi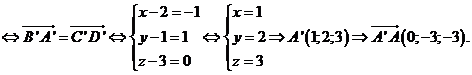
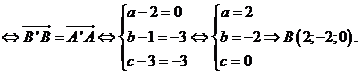
Câu 31:
 Xem đáp án
Xem đáp án
Chọn C.
Mặt cầu (S) có tâm I(1;-2;1) và bán kính R=3.
Thử A. Ta có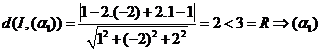 cắt (S)
cắt (S)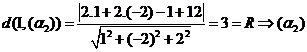 tiếp xúc với (S)
tiếp xúc với (S)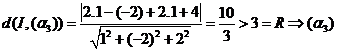 không cắt (S)
không cắt (S)Câu 32:
 Xem đáp án
Xem đáp án
Chọn D.
+ ,
+
+
Câu 33:
 Xem đáp án
Xem đáp án
Chọn D.
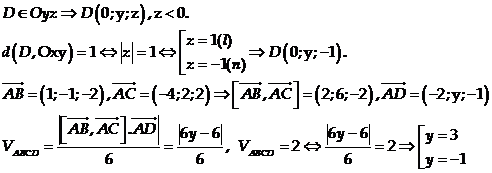
Câu 34:
 Xem đáp án
Xem đáp án
Câu 35:
 Xem đáp án
Xem đáp án
Chon A
Ta có