A. .
B. 3.
C. .
D. 2.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
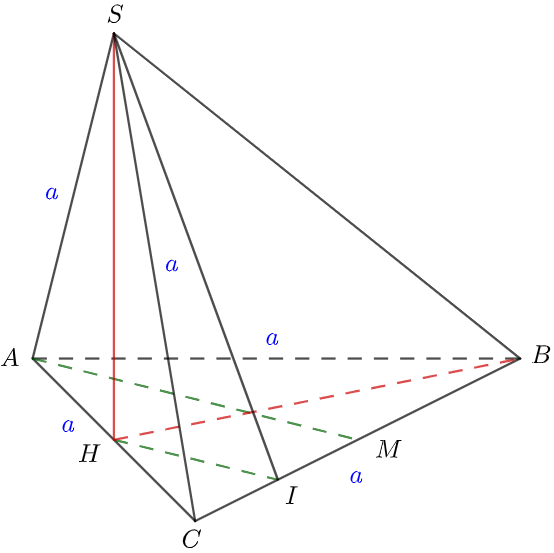
Lấy H là trung điểm của AC và tam giác ABC, tam giác SAC đều nên ta có SH AC, BH AC
(SAC) (ABC)
Tam giác ABC đều nên với M là trung điểm của BC thì ta có AM BC
Kẻ HI // AM (I BC) HI BC (*)
Kết hợp điều kiện SH BC (Do SH (ABC))
Nên suy ra BC (SHI) BC SI (**)
Từ (*) và (**) nên góc giữa hai mặt phẳng (ABC) và (SBC) chính là góc
Xét tam giác SIH vuông tại H ta có
SH và AM là đường cao của tam giác đều có cạnh bằng a nên
Từ đó suy ra
Trong mặt phẳng tọa độ Oxy, gọi (C) là đồ thị của hàm số . Phương trình tiếp tuyến của (C) tại giao điểm của đồ thị (C) với trục hoành là
Trong mặt phẳng tọa độ Oxy, gọi A, B, C, D là 4 điểm cực trị của đồ thị hàm số với hoành độ đều khác 0. Bán kính đường tròn ngoại tiếp đi qua 4 điểm A, B, C, D bằng
Trong không gian tọa độ Oxyz, gọi (P) là mặt phẳng đi qua 2 điểm A(0; 1; -2), B(2; 1; 0) sao cho khoảng cách từ gốc tọa độ O đến (P) lớn nhất. Phương trình của mặt phẳng (P) là
Cho hàm số f (x) liên tục và có đạo hàm trên [0; 1]. Biết và f (0) = f (1) = 7. Giá trị của tích phân bằng
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD và điểm O tùy ý trên mặt phẳng (BCD). Thể tích tứ diện OMNP bằng